搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为 
，则图中阴影部分的面积是 ．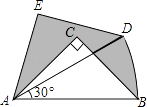 
参考答案：
【答案】
【解析】解：∵∠ACB=90°，AC=BC=1， ∴AB= 
，
∴S扇形ABD= 
= ．
又∴Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，
∴Rt△ADE≌Rt△ACB，
∴S阴影部分=S△ADE+S扇形ABD﹣S△ABC=S扇形ABD= ．
故答案为： ．
先根据勾股定理得到AB= ，再根据扇形的面积公式计算出S扇形ABD ， 由旋转的性质得到Rt△ADE≌Rt△ACB，于是S阴影部分=S△ADE+S扇形ABD﹣S△ABC=S扇形ABD
-
科目： 来源： 题型：
查看答案和解析>>【题目】(2+1)(22+1)(24+1)(28+1)(216+1)
-
科目： 来源： 题型：
查看答案和解析>>【题目】1.44的算术平方根是（ ）
A.1.2B.﹣1.2C.±1.2D.以上都是
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，若AB是⊙0的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD=（ ）
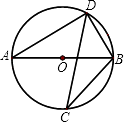
A.116°
B.32°
C.58°
D.64° -
科目： 来源： 题型：
查看答案和解析>>【题目】直线MN与直线PQ相交于O，点A在射线OP上，点B在射线OM上．
（1）如图1，
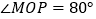已知AG、BG分别是∠BAO和∠ABO角的平分线，求
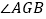的度数；（2）如图2，
已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，∠CED= 度；（3）如图3，
，过点B作直线CD⊥MN，G为射线BD上一点，OF平分∠QOG，OE⊥OF，探索
的大小是否发生变化？若不变，求其值；若改变，说明理由．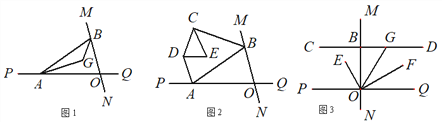
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图E在△ABC的边AC上，且∠AEB=∠ABC.
⑴求证：∠ABE=∠C；
⑵若∠BAE的平分线AF交BE于F，FD∥BC交AC于D，设AB=5，AC=8，求DC的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上
（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；
（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．
相关试题
