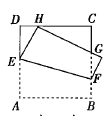
【题目】如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点AB E,交BC于点F,边AB折叠后与边BC交于点G,设正方形ABCD的周长为m,![]() 的周长为n,则
的周长为n,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.随H点位置的变化而变化
D.随H点位置的变化而变化
参考答案:
【答案】B
【解析】
设CH=x,DE=y,则DH=![]() -x,EH=
-x,EH=![]() -y,然后利用正方形的性质和折叠可以证明△DEH∽△CHG,利用相似三角形的对应边成比例可以把CG,HG分别用x,y分别表示,△CHG的周长也用x,y表示,然后在Rt△DEH中根据勾股定理可以得到
-y,然后利用正方形的性质和折叠可以证明△DEH∽△CHG,利用相似三角形的对应边成比例可以把CG,HG分别用x,y分别表示,△CHG的周长也用x,y表示,然后在Rt△DEH中根据勾股定理可以得到![]() x-x2=
x-x2=![]() y,进而求出△CHG的周长.
y,进而求出△CHG的周长.
解:设CH=x,DE=y,则DH=![]() -x,EH=
-x,EH=![]() -y,
-y,
∵∠EHG=90°,
∴∠DHE+∠CHG=90°.
∵∠DHE+∠DEH=90°,
∴∠DEH=∠CHG,
又∵∠D=∠C=90°,△DEH∽△CHG,
∴![]() ,即
,即![]() ,
,
∴CG=![]() ,HG=
,HG=![]() ,
,
△CHG的周长为n=CH+CG+HG=![]() ,
,
在Rt△DEH中,DH2+DE2=EH2
即(![]() -x)2+y2=(
-x)2+y2=(![]() -y)2
-y)2
整理得![]() -x2=
-x2=![]() ,
,
∴n=CH+HG+CG=![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M,N是以AB为直径的⊙O上的点,且
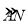 =
=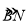 ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.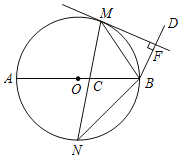
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点
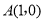 ,
,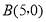 ,
,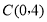 .
.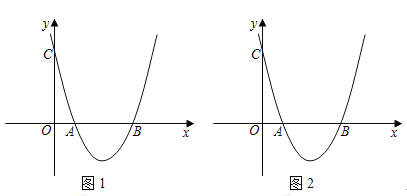
(1)求抛物线的解析式和对称轴;
(2)
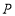 是抛物线对称轴上的一点,求满足
是抛物线对称轴上的一点,求满足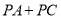 的值为最小的点
的值为最小的点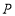 坐标(请在图1中探索);
坐标(请在图1中探索);(3)在第四象限的抛物线上是否存在点
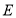 ,使四边形
,使四边形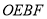 是以
是以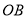 为对角线且面积为
为对角线且面积为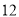 的平行四边形?若存在,请求出点
的平行四边形?若存在,请求出点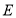 坐标,若不存在请说明理由.(请在图2中探索)
坐标,若不存在请说明理由.(请在图2中探索) -
科目: 来源: 题型:
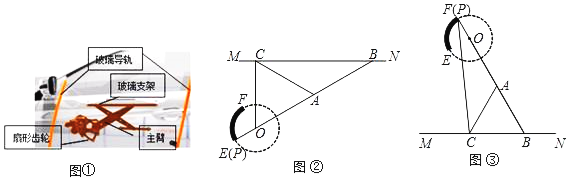
查看答案和解析>>【题目】我们常见的汽车玻璃升降器如图①所示,图②和图③是升降器的示意图,其原理可以看作是主臂PB绕固定的点O旋转,当端点P在固定的扇形齿轮
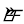 上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知
上运动时,通过叉臂式结构(点B可在MN上滑动)的玻璃支架MN带动玻璃沿导轨作上下运动而达到玻璃升降目的.点O和点P,A,B在同一直线上.当点P与点E重合时,窗户完全闭合(图②),此时∠ABC=30°;当点P与点F重合时,窗户完全打开(图③).已知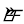 的半径OP=5cm,
的半径OP=5cm,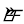 =
=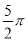 cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.(1)当窗户完全闭合时,OC=_____cm.
(2)当窗户完全打开时,PC=_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=
 ,求⊙O 的半径.
,求⊙O 的半径.
相关试题

