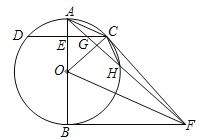
【题目】如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连接AF,CF,AF与CD交于点G,与⊙O交于点H,连接CH.
(1)求证:CF是⊙O的切线;
(2)求证:EG=GC;
(3)若cos∠AOC=![]() ,⊙O的半径为9,求CH的长.
,⊙O的半径为9,求CH的长.
参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)CH的长为![]()
【解析】试题分析:(1)根据OF∥AC,OA=OC,判断出∠BOF=∠COF;然后根据全等三角形判定的方法,判断出△BOF≌△COF,推得∠OCF=∠OBF=90°,再根据点C在⊙O上,即可判断出FC是⊙O的切线. (2)根据已知条件△AEC∽△OBF,根据相似三角形的性质可得![]() =
= ![]() ,再由∠EAG=∠BAF,∠AEG=∠ABF,可得△AEG∽△ABF,即可得
,再由∠EAG=∠BAF,∠AEG=∠ABF,可得△AEG∽△ABF,即可得![]() =
= ![]() ,因AB=2OB,所以
,因AB=2OB,所以![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,所以EC=2EG,即可得结论EG=GC ;
,所以EC=2EG,即可得结论EG=GC ;
(3)延长CO交⊙O于K,连接HK,易证∠CAF=∠HCF,再由∠AFC=∠CFH,即可判断△ACF∽△CHF,根据相似三角形的性质可得![]() =
= ![]() ,因cos∠AOC=
,因cos∠AOC= ![]() ,OC=9,可得
,OC=9,可得![]() =
= ![]() =
= ![]() ,即可求得OE=6,所以AE=3,EC 2=OC 2-OE 2=45,由勾股定理可得AC=
,即可求得OE=6,所以AE=3,EC 2=OC 2-OE 2=45,由勾股定理可得AC= ![]() =3
=3![]() ,再由
,再由![]() =
= ![]() ,可求得BF=9
,可求得BF=9![]() ,再由勾股定理可得AF=
,再由勾股定理可得AF= ![]() =27,BF、CF都是⊙O的切线,根据切线长定理可得CF=BF=9
=27,BF、CF都是⊙O的切线,根据切线长定理可得CF=BF=9![]() ,由此求得CH=
,由此求得CH=![]() .
.
试题解析:
(1)∵BF为⊙O的切线,∴∠OBF=90°
∵OA=OC,∴∠OAC=∠OCA
∵OF∥AC,∴∠OAC=∠BOF,∠OCA=∠COF
∴∠BOF=∠COF
又OB=OC,OF=OF,∴△OBF≌△OCF
∴∠OCF=∠OBF=90°
∴CF是⊙O的切线
(2)∵AB⊥CD,∴∠AEC=90°
∴∠AEC=∠OBF
又∠EAC=∠BOF,∴△AEC∽△OBF
∴![]() =
= ![]()
∵∠EAG=∠BAF,∠AEG=∠ABF
∴△AEG∽△ABF,∴![]() =
= ![]()
∵AB=2OB,∴![]() =
= ![]() ,即
,即 ![]() =
= ![]()
∴EC=2EG,∴EG=GC
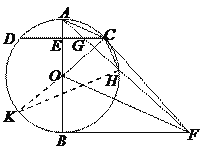
(3)延长CO交⊙O于K,连接HK
则∠K=∠CAF,∠K+∠OCH=90°
∵∠OCF=90°,∴∠HCF+∠OCH=90°
∴∠CAF=∠HCF
又∠AFC=∠CFH,∴△ACF∽△CHF,∴![]() =
= ![]()
∵cos∠AOC= ![]() ,OC=9,∴
,OC=9,∴![]() =
= ![]() =
= ![]()
∴OE=6,∴AE=3,EC 2=OC 2-OE 2=45
∴AC= ![]() =3
=3![]()
∵![]() =
= ![]() ,∴
,∴![]() =
= ![]() ,∴BF=9
,∴BF=9![]()
∴AF= ![]() =27
=27
∵BF、CF都是⊙O的切线,∴CF=BF=9![]()
∴![]() =
= ![]() ,∴CH=
,∴CH=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BD为∠ABC的平分线.
(1)如图1,∠C=2∠DBC,∠A=60°,求证:△ABC为等边三角形;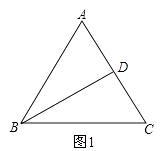
(2)如图2,若∠A=2∠C,BC=8,AB=4.8,求AD的长度;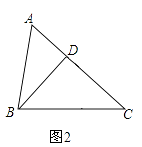
(3)如图3,若∠ABC=2∠ACB,∠ACB的平分线OC与BD相交于点O,且OC=AB,求∠A的度数.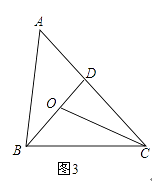
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
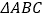 中,
中, .如图①,
.如图①,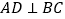 于点
于点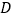 ,
,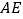 平分
平分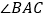 ,则易知
,则易知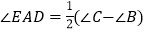 .
.(1)如图②,
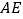 平分
平分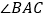 ,
, 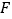 为
为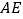 上的一点,且
上的一点,且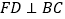 于点
于点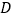 ,这时
,这时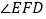 与
与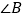 、
、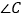 有何数量关系?请说明理由;
有何数量关系?请说明理由;(2)如图③,
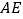 平分
平分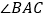 ,
,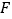 为
为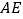 延长线上的一点,
延长线上的一点,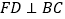 于点
于点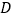 ,请你写出这时
,请你写出这时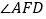 与
与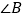 、
、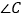 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).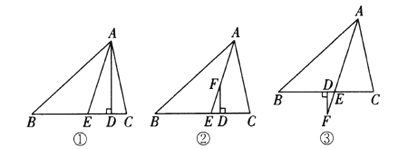
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是方程x2+ax+2=0的一个根,则a的值是( )
A.﹣2B.﹣3C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A.2a2+3a2=5a4
B.(a﹣b)2=a2﹣b2
C.(a3)3=a6
D.(﹣2a2)3=﹣8a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】小丽和小明玩数学游戏,小丽取出一个不透明的口袋,口袋中装有四张分别标有数字2,3,4,6的卡片,卡片除数字外其余都相同,小丽要求小明从中随机抽取一张卡片并记录下卡片上的数字,将卡片放回洗匀,再次从中随机抽取一张卡片,同样记录下卡片上的数字.
(1)请用画树状图或列表的方法表示小明两次抽取卡片的所有可能出现的结果;
(2)求小明抽到的两张卡片上的数都能被2整除的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 内错角相等,两直线平行B. 两直线平行,同旁内角互补
C. 相等的角是对顶角D. 等角的补角相等
相关试题

