【题目】 交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆/小时)指单位时间内通过道路指定断面的车辆数;速度
(辆/小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米/小时)指通过道路指定断面的车辆速度,密度
(千米/小时)指通过道路指定断面的车辆速度,密度![]() (辆/千米)指通过道路指定断面单位长度内的车辆数.
(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度 | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量 | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确的是____.(只填上正确答案的序号)
关系最准确的是____.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() 满足
满足![]() .请结合(1)中选取的函数关系式继续解决下列问题.
.请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵;
在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离![]() (米)均相等,求流量
(米)均相等,求流量![]() 最大时
最大时![]() 的值.
的值.
参考答案:
【答案】(1)③(2)当v=30时,q最大=1800(3)①84<k≤96②流量最大时d的值为![]() 米.
米.
【解析】
试题分析:(1)设q与v的函数关系式为q=av2+bv,依题可得二元一次方程组求出q与v的函数关系式,即可得出答案.
(2)由(1)得到的二次函数关系式,根据其图像性质即可求出答案.
(3)①根据q=vk即可得出v=-![]() k+60代入12≤v<18即可求出k的范围.
k+60代入12≤v<18即可求出k的范围.
②根据v=30时,q最大=1800,再将v值代入v=-![]() k+60求出k=60,从而得出d.
k+60求出k=60,从而得出d.
试题解析:(1)设q与v的函数关系式为q=av2+bv,依题可得:
![]() ,
,
解得![]() ,
,
∴q=-2v2+120v.
故答案为③.
(2)解:∵q=-2v2+120v=-2(v-30)2+1800.
∴当v=30时,q最大=1800.
(3)解:①∵q=vk,
∴k=![]() =
=![]() =-2v+120.
=-2v+120.
∴v=-![]() k+60.
k+60.
∵12≤v<18,
∴12≤-![]() k+60<18.
k+60<18.
解得:84<k≤96.
②∵当v=30时,q最大=1800.
又∵v=-![]() k+60,
k+60,
∴k=60.
∴d=![]() =
=![]() .
.
∴流量最大时d的值为![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由线段AB,CD,DF,BF,CA组成的平面图形,∠D=28°,则∠A+∠B+∠C+∠F的度数为( )

A.62°
B.152°
C.208°
D.236° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )

A.8
B.9
C.10
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】若|a﹣1|+(b+3)2=0,则ba=( )
A.﹣3
B.﹣1
C.3
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品.现将有关数据呈现如下图:

①
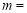 ,
,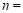 ;
;②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判定两个直角三角形全等的方法,错误的是 ( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一直角边对应相等 D. 两锐角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(3,2)在( )
A.第一象限B.第二象限C.第三象限D.第四象限
相关试题

