【题目】阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式,例如:![]() ,
,![]() ,
,![]() ,…含有两个字母
,…含有两个字母![]() ,
,![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等对称式都可以用
等对称式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
请根据以上材料解决下列问题:
(1)式子:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,属于对称式的是 (填序号)
中,属于对称式的是 (填序号)
(2)已知![]() .
.
①若![]() ,求对称式
,求对称式![]() 的值
的值
②若![]() ,求对称式
,求对称式![]() 的最大值
的最大值
参考答案:
【答案】(1)①③④;(2)①12,②-2.
【解析】
(1)根据新定义的“对称式”的意义进行判断,做出选择,
(2)已知![]() .则
.则![]() ,
,![]() ,
,
①![]() ,
,![]() ,利用整式变形可求出
,利用整式变形可求出![]() 的值;
的值;
②![]() 时,即
时,即![]() ,由
,由![]() 可以求出
可以求出![]() 的最大值;
的最大值;
解:(1)根据“对称式”的意义,得①③④是“对称式”,
故答案为:①③④,
(2)①![]() .
.
![]() ,
,![]() ,
,
①当![]() ,
,![]() 时,即
时,即![]() ,
,![]() ,
,
![]() ,
,
②当![]() 时,即
时,即![]()
![]() ,
,
所以当m=0时,![]() 有最大值-2,
有最大值-2,
故代数式![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 内,
内, ,
, ,点
,点 在
在 外,
外, ,
,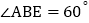 .
.(1)求
 的度数;
的度数;(2)判断
 的形状并加以证明;
的形状并加以证明;(3)连接
 ,若
,若 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数
1800
510
250
210
150
120
人数
1
1
3
5
3
2
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,∠FGH=90°,∠GHM= 40°,∠HMN=30°,并且∠EFA的两倍比∠CNP大10°,则∠PND的大小是( )

A. 100°B. 120°C. 130°D. 150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形.
乙同学:我发现边数是6时,它也不一定是正多边形,如图1,△ABC是正三角形,
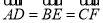 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.丙同学:我能证明,边数是5时,它是正多边形,我想…,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等;
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图2)是正七边形;(不必写已知,求证)
(3)根据以上探索过程,提出你的猜想.(不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.

相关试题

