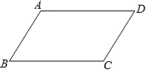
【题目】如图,平行四边形ABCD中,AD>AB
(1)分别作∠ABC和∠BCD的平分线,交AD于E、F.
(2)线段AF与DE相等吗?请证明.
参考答案:
【答案】(1)详见解析;(2)AF与DE相等,证明见解析.
【解析】
(1)根据角平分线的作法作出∠ABC和∠BCD的平分线即可;
(2)根据平行四边形的性质可得:AB=CD,AD∥BC,根据平行线性质和角平分线性质求出∠ABE=∠AEB,推出AB=AE,同理求出DF=CD,即可证明AE=DF,故AF=DE.
(1)如图:BE、CF即∠ABC和∠BCD的平分线,
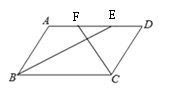
(2)解:AF与DE相等.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
同理可得:DF=CD,
∴AE=DF,
即AF+EF=DE+EF,
∴AF=DE.
故答案为:(1)详见解析;(2)AF与DE相等,证明见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:
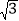 ≈1.7)
≈1.7)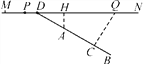
-
科目: 来源: 题型:
查看答案和解析>>【题目】请认真阅读,回答下面问题:如图,
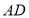 为
为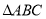 的中线,
的中线,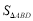 与
与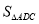 相等吗?(友情提示:
相等吗?(友情提示: 表示三角形面积)
表示三角形面积)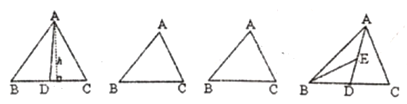
解:过
 点作
点作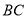 边上的高
边上的高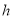 ,
,∵
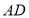 为
为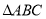 的中线
的中线∴
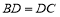
∵
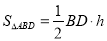
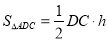
∴
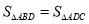
(1)用一句简洁的文字表示上面这段内容的结论;
(2)利用上面所得的结论,用不同的割法分别把下面两个三角形面积4等分,(只要割线不同就算一种)
(3)已知:
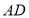 为
为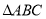 的中线,点
的中线,点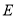 为
为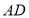 边上的中点,若
边上的中点,若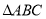 的面积为20,
的面积为20,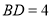 ,求点
,求点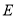 到
到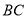 边的距离为多少?
边的距离为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c是正数,下列各式,从左到右的变形不能用如图验证的是( )

A. (b+c)2=b2+2bc+c2
B. a(b+c)=ab+ac
C. (a+b+c)2=a2+b2+c2+2ab+2bc+2ac
D. a2+2ab=a(a+2b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,BC=
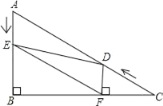
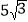 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E,D,C,B四点在平行于斑马线的同一直线上)(参考数据:tan15°=2-
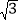 ,
,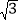 ≈1.732,
≈1.732,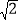 ≈1.414)
≈1.414)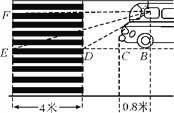
-
科目: 来源: 题型:
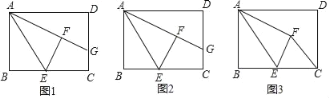
查看答案和解析>>【题目】如图,在矩形ABCD中,E是BC上一动点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,AB=3,AD=4.
(1)如图,当∠DAG=30° 时,求BE的长;
(2)如图,当点E是BC的中点时,求线段GC的长;
(3)如图,点E在运动过程中,当△CFE的周长最小时,直接写出BE的长.
相关试题

