【题目】如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论:①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=![]() ,则BH=3;⑤若DF⊥BE于点F,则AE-FH=DF;正确的有( )个.
,则BH=3;⑤若DF⊥BE于点F,则AE-FH=DF;正确的有( )个.

A. 5B. 4C. 3D. 2
参考答案:
【答案】C
【解析】
根据角平分线、高、等腰直角三角形的性质,全等三角形的性质和判定,矩形的判定和性质依次判断即可得出答案.
解:①∵∠1=∠2=22.5°,
又∵AD是高,
∴∠2+∠C=∠3+∠C,
∴∠2=∠3,
∴∠1=∠3,故①正确;
②∵∠1=∠2=22.5°,
∴∠ABD=∠BAD=45°,
∴AD=BD,
又∵∠2=∠3,∠ADB=∠ADC,
∴△BDH≌△ADC,
∴DH=CD,
∵∠1=∠2,BE⊥AC,
∴AB=BC,
∴BD+DH=AB,故②正确;
③无法证明;
④无法证明;
⑤作DG⊥AC于G,
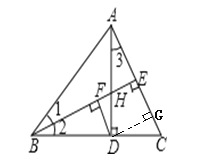
∵BE⊥AC,DF⊥BE,DG⊥AC,
∴四边形EFDG是矩形,
∴DF=EG,
∵BE⊥AC,DF⊥BE,DG⊥AC,
∴∠3+∠AHE=∠3+∠C=∠FDH+∠FHD,∠DFH=∠DGC=90°,
∵∠AHE=∠FHD,
∴∠C=∠FHD,
由②得,DH=CD,
∴△DFH≌△DGC,
∴FH=CG,
∴EC-CG=EG,即EC-FH=DF,
∵AB=BC,BE⊥AC,
∴AE=EC,
∴AE-FH=DF,故⑤正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有理数大小关系判断正确的是( )
A. 0>|﹣10| B. ﹣(﹣
 )>﹣|﹣
)>﹣|﹣ | C. |﹣3|<|+3| D. ﹣1>﹣0.01
| C. |﹣3|<|+3| D. ﹣1>﹣0.01 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.

(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=
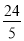 ,求BD和BC的长.
,求BD和BC的长.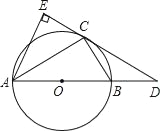
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标平面内,从点(x,y)移动到点(x+1,y+2)的运动称为一次A类跳马,从点(x,y)移动到点(x+2,y+1)的运动称为一次B类跳马.现在从原点开始出发,连续10次跳马,每次跳马采取A类或B类跳马,最后恰好落在直线
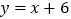 上,则最后落马的坐标是_______.
上,则最后落马的坐标是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有一条直线l:
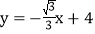 与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.
与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移.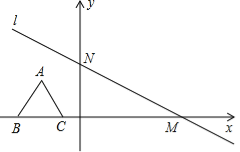
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标 ;
(2)继续向右平移,得到△A2B2C2,此时它的外心P恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地台风带来严重灾害,该市组织20辆汽车装食品、药品、生活用品三种救灾物质共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同种物质且必须装满.根据表格提供的信息,解答下列问题:
物资种类
食品
药品
生活用品
每辆汽车运载量(吨)
6
5
4
每吨所需运费(元/吨)
120
160
100
(1)若装食品的车辆是5辆,装药品的车辆为__________辆;
(2)设装食品的车辆为x辆,装药品的车辆为y辆,求y与x的函数关系式;
(3)如果装食品的车辆不少于7辆,装药品的车辆不少于4辆,那么车辆的安排有几种方案?请写出每种方案并求出最少费用.
相关试题

