搜索
【题目】下列有理数大小关系判断正确的是（ ）
A. 0＞|﹣10| B. ﹣（﹣
）＞﹣|﹣
| C. |﹣3|＜|+3| D. ﹣1＞﹣0.01
参考答案：
【答案】B
【解析】
A.首先求出|﹣10|=10，然后根据有理数大小比较的方法判断即可;B.首先判断出﹣（﹣
）=，﹣|﹣
|=﹣，然后根据有理数大小比较的方法判断即可;C.首先判断出|﹣3|=3，|+3|=3，然后根据有理数大小比较的方法判断即可;D.两个负数，绝对值大的其值反而小，据此判断即可．
∵|﹣10|=10，0＜10，
∴0＜|﹣10|，
∴选项A不正确；
∵﹣（﹣）=，﹣|﹣|=﹣，＞﹣，
∴﹣（﹣）＞﹣|﹣|，
∴选项B正确；
∵|﹣3|=3，|+3|=3，
∴|﹣3|=|+3|，
∴选项C不正确；
∵|﹣1|=1，|﹣0.01|=0.01，1＞0.01，
∴﹣1＜﹣0.01，
∴选项D不正确．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）在Rt△ABC中，∠BAC=
,D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F．
（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=4，AB=5，求菱形ADCFD 的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）的图象经过点A（3，0），B（2，﹣3），并且以x=1为对称轴．
（1）求此函数的解析式；
（2）作出二次函数的大致图象；
（3）在对称轴x=1上是否存在一点P，使△PAB中PA=PB？若存在，求出P点的坐标；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上A，B两点对应的有理数分别为xA＝﹣5和xB＝6，动点P从点A出发，以每秒1个单位的速度沿数轴在A，B之间往返运动，同时动点Q从点B出发，以每秒2个单位的速度沿数轴在B，A之间往返运动．设运动时间为t秒．
(1)当t＝2时，点P对应的有理数xP＝______，PQ＝______；
(2)当0＜t≤11时，若原点O恰好是线段PQ的中点，求t的值；
(3)我们把数轴上的整数对应的点称为“整点”，当P，Q两点第一次在整点处重合时，直接写出此整点对应的数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，△AOB是直角三角形，∠AOB=90°，边AB与y轴交于点C.
（1）若∠A=∠AOC，试说明：∠B=∠BOC；
（2）延长AB交x轴于点E，过O作OD⊥AB，若∠DOB=∠EOB，∠A=∠E，求∠A的度数；
（3）如图，OF平分∠AOM，∠BCO的平分线交FO的延长线于点P，∠A=40°，当△ABO绕O点旋转时（边AB与y轴正半轴始终相交于点C），问∠P的度数是否发生改变？若不变，求其度数；若改变，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知⊙O是△ABC的外接圆，AB是⊙O的直径，D是AB延长线上一点，AE⊥DC交DC的延长线于点E，且AC平分∠EAB．
（1）求证：DE是⊙O的切线；
（2）若AB=6，AE=
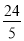，求BD和BC的长．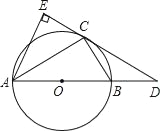
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，高AD和BE交于点H，且∠1=∠2=22.5°，下列结论：①∠1=∠3；②BD+DH=AB；③2AH=BH；④若CD=
，则BH=3；⑤若DF⊥BE于点F，则AE-FH=DF；正确的有( )个.
A. 5B. 4C. 3D. 2
相关试题
