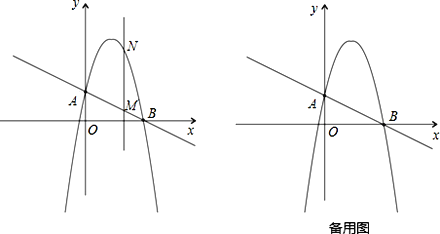
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
参考答案:
【答案】(1)抛物线解析式为![]() ;
;
(2)当 t=2 时,MN有最大值为 4;
(3)D(0,6)或(0,-2)或(4,4).
【解析】试题分析:
(1)先由直线![]() 分别交y轴、x轴于点A、B这一条件求出点A、B的坐标,将所求坐标代入抛物线
分别交y轴、x轴于点A、B这一条件求出点A、B的坐标,将所求坐标代入抛物线![]() 列出关于
列出关于![]() 的值即可得到所求抛物线的解析式;
的值即可得到所求抛物线的解析式;
(2)如图1,由题意可知点M的横坐标为t,根据点M在直线![]() 上,点N在(1)中所求抛物线上,可用含“t”的代数式表达出点M、N的坐标,结合第一象限中,点N在点M的上方,可用含“t”的代数式表达出MN的长,把所得式子配方,即可得到所求答案;
上,点N在(1)中所求抛物线上,可用含“t”的代数式表达出点M、N的坐标,结合第一象限中,点N在点M的上方,可用含“t”的代数式表达出MN的长,把所得式子配方,即可得到所求答案;
(3)由(2)中答案可得求得对应的点A、M、N的坐标,如图2分析可知点D有三种可能,其中两种情况点D在y轴上,结合AD=MN,即可求得两个符合要求的点D1、D2的坐标;由图可知第三个符合要求点D就是直线D1N和D2M的交点,求出两直线的解析式联立成方程组,解方程组即可求得第三个符合要求的点D的坐标.
试题解析:
(1)∵![]() 分别交y轴、x轴于A.、B两点,
分别交y轴、x轴于A.、B两点,
∴A、B点的坐标为:A(0,2),B(4,0),
将x=0,y=2代入y=x+bx+c得c=2,
将x=4,y=0,c=2代入y=x+bx+c得0=16+4b+2,解得b=![]() ,
,
∴抛物线解析式为: ![]() ,
,
(2)如图1,由题意可知,直线MN即是直线![]() ,
,
∵点M在直线![]() 上,点N在抛物线
上,点N在抛物线![]() 上,
上,
∴点M、N的坐标分别为![]() 、
、![]() ,
,
∵在第一象限中,点N在点M的上方,
∴MN=![]() ,
,
∴当![]() 时,MN最长=4;
时,MN最长=4;
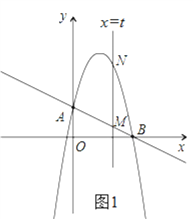
(3)由(2)可知,A(0,2),M(2,1),N(2,5).
以A. M、N、D为顶点作平行四边形,D点的可能位置有三种情形,如图2所示:
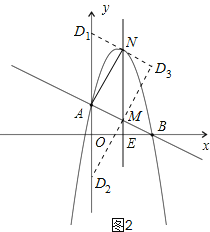
(i)当D在y轴上时,设D的坐标为(0,a)
由AD=MN,得|a2|=4,解得a1=6,a2=2,
从而D1为(0,6)或D2(0,2),
(ii)当D不在y轴上时,由图可知D3为D1N与D2M的交点,
由D1、D2、M、N的坐标可求得直线D1N的解析式为:y=![]() x+6,直线D2M的解析式为:y=
x+6,直线D2M的解析式为:y=![]() x2,
x2,
由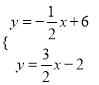 解得
解得![]() ,
,
∴D3的坐标为:(4,4),
综上所述,所求的D点坐标为(0,6),(0,2)或(4,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+
x+ 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
A. 2B. 4C. 6D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC与△ADE中,AB=AC,AD=AE,∠A是公共角。
(1)BD与CE的数量关系是:BD______CE;
(2)把图①△ABC绕点A旋转一定的角度,得到如图②所示的图形。
①求证:BD=CE;
②BD与CE所在直线的夹角与∠DAE的数量关系是什么?说明理由。
(3)若AD=10,AB=6,把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的
高度CD为100m,点A、D、B在同一直线上,CD⊥AB,则A、B两点的距离是( )

A. 200m B. 200
 m C.
m C.  m D.
m D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形
 中,
中, ,点
,点 分别是
分别是 的中点. 已知两底之差是6,两腰之和是12,则
的中点. 已知两底之差是6,两腰之和是12,则 的周长是____.
的周长是____. 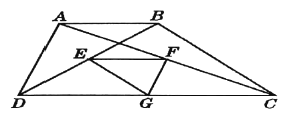
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个不透明的袋子分别装有红、白两种颜色的球(除颜色不同外其余均相同),甲袋中有2个红球和1个白球,乙袋中有1个红球和3个白球.
(1)如果在甲袋中随机摸出一个小球,那么摸到红球的概率是______.
(2)如果在乙袋中随机摸出两个小球,那么摸到两球颜色相同的概率是______.
(3)如果在甲、乙两个袋子中分别随机摸出一个小球,那么摸到两球颜色相同的概率是多少?(请用列表法或树状图法说明)
相关试题

