搜索
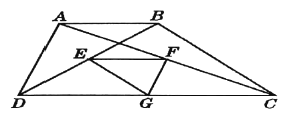
【题目】如图，梯形
中，
，点
分别是
的中点. 已知两底之差是6，两腰之和是12，则
的周长是____.
参考答案：
【答案】9.
【解析】
延长EF交BC于点H，可知EF，FH，FG、EG分别为△BDC、△ABC、△BDC和△ACD的中位线，由三角形中位线定理结合条件可求得EF+FG+EG，可求得答案．
连接AE，并延长交CD于K，
∵AB∥CD，
∴∠BAE=∠DKE，∠ABD=∠EDK，
∵点E、F、G分别是BD、AC、DC的中点．
∴BE=DE，
在△AEB和△KED中，
，
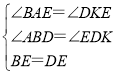∴△AEB≌△KED（AAS），
∴DK=AB，AE=EK，EF为△ACK的中位线，
∴EF=
CK=（DC-DK）=（DC-AB），
∵EG为△BCD的中位线，∴EG=BC，
又FG为△ACD的中位线，∴FG=AD，
∴EG+GF=（AD+BC），
∵两腰和是12，即AD+BC=12，两底差是6，即DC-AB=6，
∴EG+GF=6，FE=3，
∴△EFG的周长是6+3=9．
故答案为：9．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC与△ADE中，AB=AC，AD=AE，∠A是公共角。
（1）BD与CE的数量关系是：BD______CE；
（2）把图①△ABC绕点A旋转一定的角度，得到如图②所示的图形。
①求证：BD＝CE；
②BD与CE所在直线的夹角与∠DAE的数量关系是什么？说明理由。
（3）若AD=10，AB=6，把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数
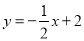分别交y轴、x 轴于A、B两点，抛物线
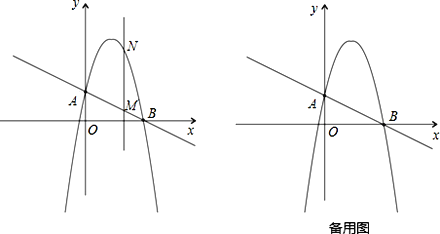
过A、B两点.（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于点M，交这个抛物线于点N.求当t 取何值时，MN有最大值？最大值是多少？
（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的
高度CD为100m,点A、D、B在同一直线上,CD⊥AB,则A、B两点的距离是( ）
A. 200m B. 200
m C. 
m D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】有两个不透明的袋子分别装有红、白两种颜色的球（除颜色不同外其余均相同），甲袋中有2个红球和1个白球，乙袋中有1个红球和3个白球.
（1）如果在甲袋中随机摸出一个小球，那么摸到红球的概率是______.
（2）如果在乙袋中随机摸出两个小球，那么摸到两球颜色相同的概率是______.
（3）如果在甲、乙两个袋子中分别随机摸出一个小球，那么摸到两球颜色相同的概率是多少？（请用列表法或树状图法说明）
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填入相应的集合.
－17，6.8，＋48，0，
，－7.9，－π，－5，－
，
，29，－20%正数集合:{________________________________…};
负分数集合:{________________________________…};
整数集合:{________________________________…}.
非负整数集合{________________________________…}.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动。
（1）运动1秒时，数轴上点B表示的数是______点P表示的数是______；
（2）动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q时出发．求：
①当点P运动多少秒时，点P与点Q相遇？
②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？
相关试题
