Question

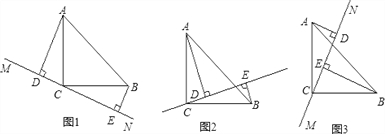
【题目】在△ABC中,∠ACB=90AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.

(1)当MN绕点C旋转到图1的位置时,请你探究线段DE、AD、BE之间的数量关系(直接写出结论,不要求写出证明过程)；

(2)当MN绕点C旋转到图2的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想，并加以证明；

(3)当MN绕点C旋转到图3的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想，并加以证明。

Answer 1

【答案】见解析

【解析】【试题分析】

（1）思路先证明△ACD≌△CBE.（AAS）再利用全等三角形的性质对应边相等，得AD=CE,CD=BE,则DE=AD+BE.

（2）思路同（1），这是第（1）题的变式，实质问题没变。

（3）这是（1）问题的变式，实质问题没变。

【试题解析】

（1）DE=AD+BE.

（2）猜想：(1)中得到的结论发生了变化。

证明：∵AD⊥MN，BE⊥MN，

∴∠ADC=∠CEB=90°.

∴∠BCE+∠CBE=90°.

∵∠ACB=90°，

∴∠ACD+∠BCE=90°.

∴∠ACD=∠CBE.

∵AC=CB，

∴△ACD≌△CBE.

∴AD=CE,CD=BE.

∵DE=CECD，

∴DE=ADBE.

(3)如图3，

猜想：(1)中得到的结论发生了变化。

证明：∵AD⊥MN，BE⊥MN，

∴∠ADC=∠CEB=90°.

∴∠BCE+∠CBE=90°.

∵∠ACB=90°，

∴∠ACD+∠BCE=90°.

∴∠ACD=∠CBE.

∵AC=CB，

∴△ACD≌△CBE.

∴AD=CE,CD=BE.

∵DE=CDCE，

∴DE=BEAD.