【题目】有下列四个条件:①AB=BC,②∠ABC=90![]() ,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
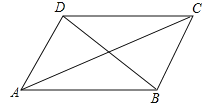
A. ②③ B. ②④ C. ①② D. ①③
参考答案:
【答案】A
【解析】分析:利用矩形、菱形、正方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.
详解:A.∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当③AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意;
B.∵四边形ABCD是平行四边形,∴当②∠ABC=90°时,平行四边形ABCD是矩形,当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意;
C.∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
D.∵四边形ABCD是平行四边形,当①AB=BC时,平行四边形ABCD是菱形,当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,□ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
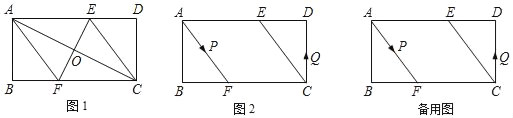
(1)如图1,连接AF、CE.求证:四边形AFCE为平行四边形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4-
 m=-m; (2)56-8x=11+x;
m=-m; (2)56-8x=11+x;(3)
 x+1=5+
x+1=5+ x; (4)-5x+6+7x=1+2x-3+8x.
x; (4)-5x+6+7x=1+2x-3+8x. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程
 ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与 对应的点,分别记作A,B;
对应的点,分别记作A,B;(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(﹣1)2017+π0﹣( )﹣1+
)﹣1+  .
.
(2)化简:(1+ )÷
)÷ 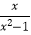 .
. -
科目: 来源: 题型:
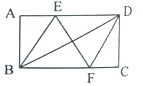
查看答案和解析>>【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为 ( )
A.
 B. 2
B. 2 C. 3
C. 3 D. 6
D. 6
相关试题

