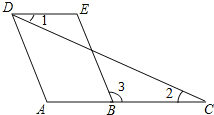
【题目】已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E.请完成解答过程.
证明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (两直线平行,内错角相等)
∴∠A=∠E(等量代换)
参考答案:
【答案】3,两直线平行,同位角相等,DE,内错角相等,两直线平行,E.
【解析】
根据平行线的性质与判定即可求解.
证明:∵AD∥BE(已知),
∴∠A=∠3(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴AC∥DE(内错角相等,两直线平行),
∴∠3=∠E(两直线平行,内错角相等),
∴∠A=∠E(等量代换),
故答案为:3,两直线平行,同位角相等,DE,内错角相等,两直线平行,E.
-
科目: 来源: 题型:
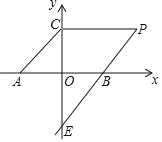
查看答案和解析>>【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线,且∠AOC=40°,∠BON=25°.
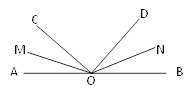
求:(1)∠COD的度数;
(2)∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华优秀传统文化,某中学在2019年元旦前夕,由校团委组织全校学生开展了一次书法比赛为了表彰书法比赛中的获奖学生,计划购买钢笔30支,毛笔20支,共需1070元,其中每支毛笔比钢笔贵6元.
(1)求钢笔和毛笔的单价各为多少元?
(2)后来校团委决定调整设奖方案,扩大表彰面,需要购买上面的两种笔共60支(每种笔的单价不变)张老师做完预算后,向财务处王老师说:“我这次买这两种笔需要支领1322元”王老师核算了一下,说:“如果你用这些钱只买这两种笔,那么账肯定算错了.”请你用学过的方程知识解释:王老师为什么说张老师用这些钱只买两种笔的账算错了.
-
科目: 来源: 题型:
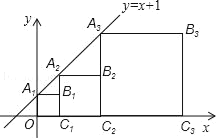
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2…、正方形AnBnnCn﹣1按如图方式放置,点A1、A2、A3、…在直线y=x+1上,点C1、C2、C3、…在x轴上.已知A1点的坐标是(0,1),则点B3的坐标为_____,点Bn的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对七年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如下所示:
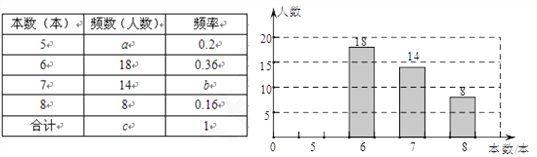
(1)统计表中的a=________,b=___________,c=____________;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校七年级共有1200名学生,请你分析该校七年级学生课外阅读7本及以上的人数.
-
科目: 来源: 题型:
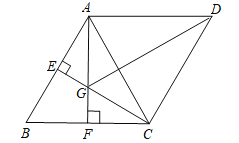
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别是AB、BC的中点,CE⊥AB,垂足为E,AF⊥BC,垂足为F,AF与CE相交于点G.
(1)证明:△CFG≌△AEG.
(2)若AB=4,求四边形AGCD的对角线GD的长.
相关试题

