【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
参考答案:
【答案】
(1)解:∵标号分别为1,2,3,4的四个球中奇数为1,3,共2个,
∴P(摸到标号数字为奇数)= ![]() =
= ![]()
(2)解:列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
所有等可能的情况数有16中,其中同为偶数或奇数的情况有:(1,1),(3,1),(2,2),(4,2),(1,3)(3,3),(2,4),(4,4),共8种情况;一奇一偶的情况有:(2,1),(4,1),(1,2),(3,2),(2,3),(4,3),(1,4),(3,4),共8种,
∴P(甲获胜)=P(乙获胜)= ![]() =
= ![]() ,
,
则这个游戏对甲、乙两人公平
【解析】(1)根据四个球中奇数的个数,除以总个数得到所求概率即可;(2)列表得出所有等可能的情况数,找出两次摸出标号数字同为奇数或偶数的情况数,以及一奇一偶的情况数,分别求出两人获胜的概率,比较即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高科技创新意识,我市某中学举行了“2016年科技节”活动,其中科技比赛包括“航模”、“机器人”、“环保”“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有人;
(2)将条形统计图补充完整;
(3)“建模”在扇形统计图中的圆心角是°. -
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
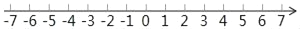
(1)数轴上表示5与﹣2两点之间的距离是
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(4)由以上探索猜想|x+10|+|x+2|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
(5)由以上探索猜想|x+10|+|x+2|+|x﹣8|+|x﹣10|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l交x轴于点C,交y轴于点D,与反比例函数y=
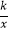 (k>0)的图像交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3
(k>0)的图像交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3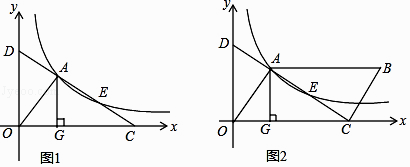
(1)k=;
(2)求证:AD=CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题共6分)已知在纸面上有一数轴(如图所示).

操作一:
(1)折叠纸面,使数1表示的点与数﹣1表示的点重合,则此时数﹣2表示的点与数 表示的点重合;
操作二:
(2)折叠纸面,使数5表示的点与数﹣1表示的点重合,回答下列问题:
①数6表示的点与数 表示的点重合;
②若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(A在B的左侧),则A点表示的数为 ,B点表示的数为 .
-
科目: 来源: 题型:
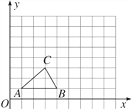
查看答案和解析>>【题目】如图,在9×9网格中,每个小方格的边长看作单位1,每个小方格的顶点叫作格点,△ABC的顶点都在格点上.
(1)请在网格中画出△ABC的一个位似图形△A1B1C,使两个图形以点C为位似中心,且所画图形与△ABC的相似比为2∶1;
(2)将△A1B1C绕着点C顺时针旋转90°得△A2B2C,画出图形,并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标.
相关试题

