【题目】如图1,直线l交x轴于点C,交y轴于点D,与反比例函数y= ![]() (k>0)的图像交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3
(k>0)的图像交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3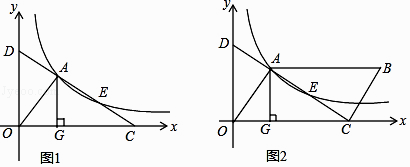
(1)k=;
(2)求证:AD=CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积.
参考答案:
【答案】
(1)6
(2)
证明:如图1中,作AN⊥OD于N,EM⊥OC于M.设直线CD的解析式为y=kx+b,A(x1,y1),E(x2,y2).
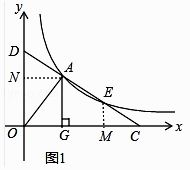
则有y1=kx1+b,y2=kx2+b,
∴y2﹣y1=k(x2﹣x1),
∴ ![]() ﹣
﹣ ![]() =k(x2﹣x1),
=k(x2﹣x1),
∴﹣kx1x2=3,
∴﹣kx1= ![]() ,
,
∴y2=﹣kx1,
∴EM=﹣kAN,
∵D(0,b),C(﹣ ![]() ,0),
,0),
∴tan∠DCO= ![]() =﹣k=
=﹣k= ![]() ,
,
∴EM=﹣kMC,
∴AN=CM,
∵AN∥CM,
∴∠DAN=∠ECM,
在△DAN和△ECM中,
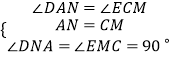 ,
,
∴△DAN≌△ECM,
∴AD=EC
(3)
解:如图2中,连接GD,GE.
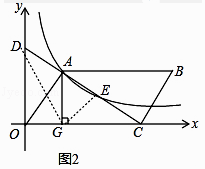
∵EA=EC,AD=EC,
∴AD=AE=EC,
∴S△ADG=S△AGE=S△GEC=3,
∵S△AOG=S△ADG=3,
∴S△AOC=3+3+3=9,
∴平行四边形ABCD的面积=2S△AOC=18
【解析】(1)解:设A(m,n),
∵ ![]() OGAG=3,
OGAG=3,
∴ ![]() mn=3,
mn=3,
∴mn=6,
∵点A在y= ![]() 上,
上,
∴k=mn=6.
所以答案是6.
【考点精析】掌握全等三角形的性质是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高科技创新意识,我市某中学举行了“2016年科技节”活动,其中科技比赛包括“航模”、“机器人”、“环保”“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有人;
(2)将条形统计图补充完整;
(3)“建模”在扇形统计图中的圆心角是°. -
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
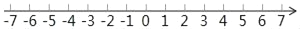
(1)数轴上表示5与﹣2两点之间的距离是
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(4)由以上探索猜想|x+10|+|x+2|+|x﹣8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
(5)由以上探索猜想|x+10|+|x+2|+|x﹣8|+|x﹣10|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里有标号分别为1,2,3,4的四个球,这些球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题共6分)已知在纸面上有一数轴(如图所示).

操作一:
(1)折叠纸面,使数1表示的点与数﹣1表示的点重合,则此时数﹣2表示的点与数 表示的点重合;
操作二:
(2)折叠纸面,使数5表示的点与数﹣1表示的点重合,回答下列问题:
①数6表示的点与数 表示的点重合;
②若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(A在B的左侧),则A点表示的数为 ,B点表示的数为 .
-
科目: 来源: 题型:
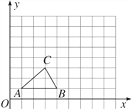
查看答案和解析>>【题目】如图,在9×9网格中,每个小方格的边长看作单位1,每个小方格的顶点叫作格点,△ABC的顶点都在格点上.
(1)请在网格中画出△ABC的一个位似图形△A1B1C,使两个图形以点C为位似中心,且所画图形与△ABC的相似比为2∶1;
(2)将△A1B1C绕着点C顺时针旋转90°得△A2B2C,画出图形,并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:

由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为 km,流动加油车出发位置为 km;
(2)当两车同时开出x小时时,甲车位置为 km,流动加油车位置为 km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
相关试题

