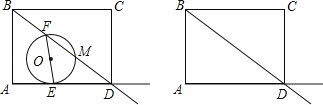
【题目】如图,矩形ABCD中,AB=6,AD=8.动点E,F同时分别从点A,B出发,分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动的时间为t.
(1)当点E在线段AD上时,用关于t的代数式表示DE,DM.
(2)在整个运动过程中,
①连结CM,当t为何值时,△CDM为等腰三角形.
②圆心O处在矩形ABCD内(包括边界)时,求t的取值范围,并直接写出在此范围内圆心运动的路径长.
参考答案:
【答案】(1)(1)ED=8﹣t,MD=![]() .(2)①t=
.(2)①t=![]() 或t=
或t=![]() 或t=
或t=![]() ;②0≤t≤
;②0≤t≤![]() ,圆心运动的路径长为
,圆心运动的路径长为![]()
【解析】
(1)在Rt△ABD中,依据勾股定理可求得BD的长,然后依据MD=EDcos∠MDE,cos∠MDE=cos∠ADB=![]() ,由此即可解决问题.
,由此即可解决问题.
(2)①可分为点E在AD上,点E在AD的延长线上画出图形,然后再依据MC=MD,CM=CD、DM=DC三种情况求解即可;
②当t=0时,圆心O在AB边上.当圆心O在CD边上时,过点E作EH∥CD交BD的延长线与点H.先求得DH的长,然后依据平行线分线段成比例定理可得到DF=DH,然后依据DF=DH列出关于t的方程,从而可求得t的值,故此可得到t的取值范围.
解:(1)如图1所示:连接ME.

∵AE=t,AD=8,
∴ED=AD-AE=8-t.
∵EF为⊙O的直径,
∴∠EMF=90°.
∴∠EMD=90°.
∴MD=EDcos∠MDE=![]() .
.
(2)①a、如图2所示:连接MC.
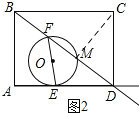
当DM=CD=6时,![]() =6,解得t=
=6,解得t=![]() ;
;
b、如图3所示:当MC=MD时,连接MC,过点M作MN⊥CD,垂足为N.

∵MC=MD,MN⊥CD,
∴DN=NC.
∵MN⊥CD,BC⊥CD,
∴BC∥MN.
∴M为BD的中点.
∴MD=5,即![]() =5,解得t=
=5,解得t=![]() ;
;
c、如图4所示:CM=CD时,过点C作CG⊥DM.

∵CM=CD,CG⊥MD,
∴GD![]() MD=
MD=![]() .
.
∵![]() ,
,
∴DG=![]() CD=
CD=![]() .
.
∴![]() =
=![]() .
.
解得:t=-1(舍去).
d、如图5所示:当CD=DM时,连接EM.
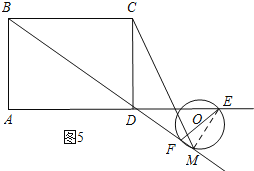
∵AE=t,AD=8,
∴DE=t-8.
∵EF为⊙O的直径,
∴EM⊥DM.
∴DM=EDcos∠EDM=![]() .
.
∴![]() =6,解得:t=
=6,解得:t=![]() .
.
综上所述,当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,△DCM为等腰三角形.
时,△DCM为等腰三角形.
②当t=0时,圆心O在AB边上.
如图6所示:当圆心O在CD边上时,过点E作EH∥CD交BD的延长线与点H.
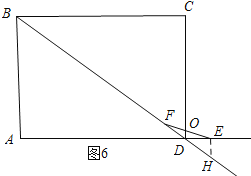
∵HE∥CD,OF=OE,
∴DF=DH.
∵DH=![]() =
=![]() ,DF=10-t,
,DF=10-t,
∴![]() =10-t.
=10-t.
解得:t=![]() .
.
综上所述,在整个运动过程中圆心O处在矩形ABCD内(包括边界)时,t的取值范围为0≤t≤![]() .
.
此时点O的运动路径为OO1的长度,如图:
过点O作OM⊥AB
当t=![]() 时,DE=
时,DE=![]() -8=
-8=![]()
∵EH∥CD,AB∥CD
∴EH∥AB
∴△DEH∽△DAB
∴![]() ,即
,即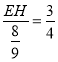 ,解得EH=
,解得EH=![]()
∴OD=![]() EH=
EH=![]()
由题意可知四边形ADOK是矩形
∴AK= OD =![]() ,OK=AD=8
,OK=AD=8
∴O1K= O1A- AK=![]()
在Rt△OKO1中,OO1=![]()
∴圆心运动的路径长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=
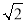 .
.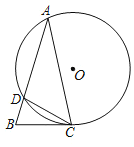
(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量
 (件)与销售单价
(件)与销售单价 (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求
 与
与 之间的函数关系式;
之间的函数关系式;(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【题目】如图①,一次函数 y=
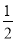 x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=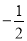 x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.(1)求二次函数的关系式及点 C 的坐标;
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
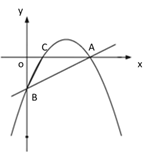
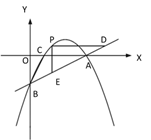
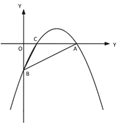
① ② ③
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,
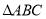 的三个顶点都在边长为
的三个顶点都在边长为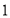 的小正方形的格点上,关
的小正方形的格点上,关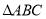 于
于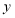 轴的对称图形为
轴的对称图形为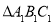 ,以
,以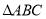 与
与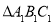 组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形
组成一个基本图形,不断复制与平移这个基本图形,得到图形所示的图形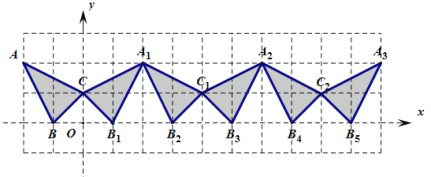
(1)观察以上图形并填写下列各点坐标:
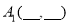 ,
,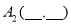 ,
, ,
,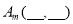 (
(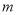 为正整数)
为正整数)(2)若
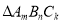 是这组图形中的一个三角形,当
是这组图形中的一个三角形,当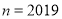 时,则
时,则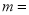 ,
,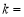
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解中学生规范书写汉字情况,某市语言文字工作委员会从市区初中在校生中抽取了部分学生进行了调查,把调查的结果分为四个等级:
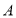 级:优秀;
级:优秀;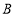 级:良好;
级:良好;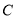 级:合格;
级:合格;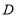 级:不合格,并绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
级:不合格,并绘制了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:(1)求本次抽样调查的学生人数;
(2)求图
 中
中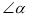 的度数,并把图
的度数,并把图 补充完整;
补充完整;(3)调查人员想从
 位同学(分别记为
位同学(分别记为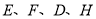 ,其中
,其中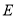 为小明)中随机选择两位同学,参加中学生提高书写汉字水平的座谈会,请用列表或画树状图的方法求出选中小明的概率.
为小明)中随机选择两位同学,参加中学生提高书写汉字水平的座谈会,请用列表或画树状图的方法求出选中小明的概率.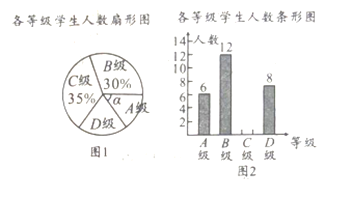
-
科目: 来源: 题型:
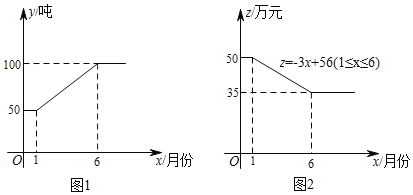
查看答案和解析>>【题目】随着技术的发展进步,某公司2018年采用的新型原料生产产品.这种新型原料的用量y(吨)与月份x之间的关系如图1所示,每吨新型原料所生产的产品的售价z(万元)与月份x之间的关系如图2所示.已知将每吨这种新型原料加工成的产品的成本为20万元.
(1)求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;
(2)若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?
相关试题

