【题目】(1)已知四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正方形边上的两个动点,点
是正方形边上的两个动点,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向运动,点
方向运动,点![]() 同时从点
同时从点![]() 出发以
出发以![]() 速度沿
速度沿![]() 方向运动.设点
方向运动.设点![]() 运动的时间为
运动的时间为![]() .
.
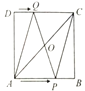
①如图1,点![]() 在
在![]() 边上,
边上,![]() 相交于点
相交于点![]() ,当
,当![]() 互相平分时,求
互相平分时,求![]() 的值;
的值;
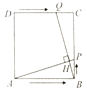
②如图2,点![]() 在
在![]() 边上,
边上,![]() 相交于点
相交于点![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
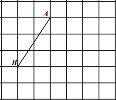
(2)如图,在小正方形的边长为1的正方形网格中,点![]() 在格点上.
在格点上.
①线段![]() 的长是_____________;
的长是_____________;
②在网格中用无刻度的直尺,以![]() 为边画矩形
为边画矩形![]() ,使这个矩形的面积是
,使这个矩形的面积是![]() .
.
要求:保留画图痕迹,并说明点![]() 的位置如何找到的.
的位置如何找到的.
参考答案:
【答案】(1)①2;②4;(2)①![]() ;②见详解.
;②见详解.
【解析】
(1)①根据![]() 互相平分得四边形APCQ为平行四边形,进而可得AP=CQ,列出方程求解即可;
互相平分得四边形APCQ为平行四边形,进而可得AP=CQ,列出方程求解即可;
②根据![]() 结合∠ABC=∠C=90°及AB=BC可证得△ABP≌△BCQ,进而可得BP=CQ,列出方程求解即可;
结合∠ABC=∠C=90°及AB=BC可证得△ABP≌△BCQ,进而可得BP=CQ,列出方程求解即可;
(2)①利用勾股定理计算即可;
②先利用勾股定理求得AB的长为![]() ,再结合矩形的面积是
,再结合矩形的面积是![]() 求得矩形另一组边长为
求得矩形另一组边长为![]() ,也就是AB的长的一半,进而可以先作出以AB为边的正方形ABEF,再找到BE、AF的中点C、D,连接CD,则矩形ABCD即为所求.
,也就是AB的长的一半,进而可以先作出以AB为边的正方形ABEF,再找到BE、AF的中点C、D,连接CD,则矩形ABCD即为所求.
解:(1)①如图1,由题意得:AP=2t,DQ=t,
∵正方形ABCD的边长为6,
∴CQ=CD-DQ=6-t,
∵PQ与AC互相平分,
∴四边形APCQ为平行四边形,
∴AP=CQ,
∵AP=2t,CQ=6-t,
∴2t=6-t,
解得:t=2(符合题意);
②如图2,由题意得:BP=2t-6,CQ=6-t,
∵AP⊥BQ,
∴∠AHB=90°,
∴∠PAB+∠ABH=90°,
∵在正方形ABCD中,∠ABC=∠C=90°,AB=BC
∴∠QBC+∠ABH=90°,
∴∠QBC=∠PAB,
∴在△QBC和△PAB中,
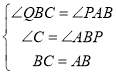
∴△QBC≌△PAB(AAS),
∴CQ=BP,
∴2t-6=6-t,
解得:t=4(符合题意);
(2)①如图,由题意得:AP=3,BP=2,
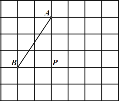
∴在Rt△ABP中,![]() ;
;
②如图,矩形ABCD即为所求,
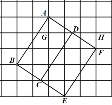
理由如下:由图结合①可知:在正方形ABEF中,BE=AB=AF=![]() ,∠ABC=90°,
,∠ABC=90°,
∵在△AGD和△FHD中,
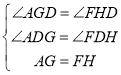
∴△AGD≌△FHD(AAS),
∴AD=FD=![]() AF=
AF=![]() ,
,
同理可得BC=CE=![]() BE=
BE=![]() ,
,
∴AD=BC,
∵在正方形ABEF中,AF∥BE即AD∥BC,
∴四边形ABCD为平行四边形,
又∵∠ABC=90°,
∴四边形ABCD为矩形,
∵S矩形ABCD=AB·AD=![]() ,
,
∴矩形ABCD即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
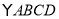 中,
中,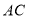 、
、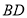 相交于点
相交于点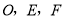 分别是
分别是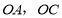 中点,连接
中点,连接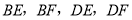 .
.(1)如图1,求证:四边形
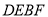 是平行四边形;
是平行四边形;(2)如图2,若
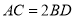 ,求证:四边形
,求证:四边形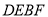 是矩形.
是矩形.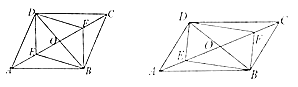
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在矩形
 中,
中,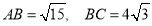 .求:①矩形
.求:①矩形 的面积
的面积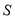 ;②对角线
;②对角线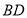 的长.
的长.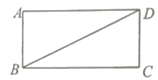
(2)如图,在菱形
 中,
中,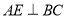 ,
,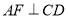 ,
,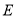 ,
,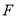 为垂足.
为垂足.①求证:
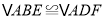 .
.②若
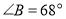 ,求
,求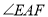 的大小.
的大小.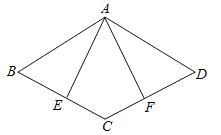
-
科目: 来源: 题型:
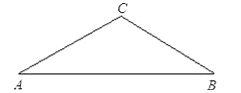
查看答案和解析>>【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
-
科目: 来源: 题型:
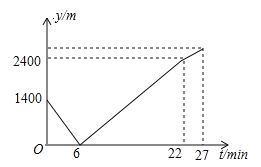
查看答案和解析>>【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到
 的位置,
的位置, ,
, ,平移距离为6,则阴影部分面积为
,平移距离为6,则阴影部分面积为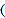


A. 24 B. 40 C. 42 D. 48
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC的两个顶点坐标为A(-3,0),B(3,0),则点
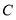 的坐标为____,△ABC的面积为____.
的坐标为____,△ABC的面积为____.
相关试题

