搜索
【题目】小毅和小明同时从学校出发到科技馆参加活动，小毅每小时走6千米，小明每小时走8千米，走了1小时后，小明忘带材料返回学校取材料，立即按原路去追小毅．小明几小时追上小毅？
参考答案：
【答案】小明3小时追上小毅．
【解析】试题分析：利用小明与小毅的时间差值为1小时，进而根据路程相等列出方程求出即可．
解：设小明x小时追上小毅，可得：
8x=6（x+1），
解得：x=3．
答：小明3小时追上小毅．
-
科目： 来源： 题型：
查看答案和解析>>【题目】方程x2﹣9=0的解是（ ）
A. x=3 B. x=﹣3 C. x=±9 D. x1=3，x2=﹣3
-
科目： 来源： 题型：
查看答案和解析>>【题目】种一批树苗，如果每人种10棵，则剩6棵树苗未种，如果每人种12棵，则缺14棵树苗．问有多少人参加种树？设有x人参加种树，可列出方程 ______ ．
-
科目： 来源： 题型：
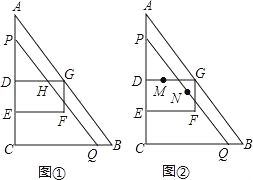
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，点D、E在边AC上，AD=4cm，点E是CD的中点，以DE为边的矩形DEFG的顶点G在边AB上，动点P从点A出发，以1cm/s的速度沿AC向点C运动，过点P作PQ∥AB交BC于点Q，设点P的运动时间为t（s），矩形DEFG与△PCQ重叠部分图形的面积为s（cm2）．
（1）在点P的运动过程中，当线段PQ与矩形DEFG的边DG有交点，令交点为H，用含t的代数式表示线段DH的长．
（2）求s与t的函数关系式．
（3）点P出发的同时，动点M从点D出发，以acm/s的速度沿D-G-F-E-F运动，点N是线段PQ中点，在点P的运动过程中，若点M、N能够重合在矩形DEFG的边上，求动点M的速度a．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若等腰三角形中有一个角等于50°，则其它两个角的度数为（ ）。
A.70°
B.50°和80或65°和65°
C.65°和65°
D.50°和80° -
科目： 来源： 题型：
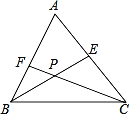
查看答案和解析>>【题目】如图，在△ABC中，∠ABC和∠ACB的平分线BE、CF相交于点P．
（1）若∠ABC=70°，∠ACB=50°，则∠BPC= °；
（2）求证：∠BPC=180°﹣
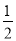（∠ABC+∠ACB）；（3）若∠A=α，求∠BPC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠A∶∠B∶∠C=1∶1∶2，则△ABC的形状是（ ）.
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等边三角形
相关试题
