【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由于∠AEF是直角,则∠BAE和∠FEC同为∠AEB的余角,由此得证;
(2)根据正方形的性质,易证得AG=EC,∠AGE=∠ECF=135°;再加上(1)得出的相等角,可由ASA判定两个三角形全等;
(3)在Rt△ABE中,根据勾股定理易求得AE2;由(2)的全等三角形知:AE=EF,即△AEF是等腰Rt△,因此其面积为AE2的一半,由此得解
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1 , 另有一次函数y=x+b的图象记为y2 , 则以下说法: ①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m< ;
;
③当m=﹣b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为 .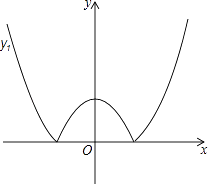
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m1=
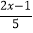 ,m2=﹣x+3.
,m2=﹣x+3.(1)若m1与m2互为相反数,求x的值;
(2)若m1是m2的2倍,求x的值;
(3)若m2比m1小1,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算: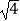 +(π﹣1)0﹣(
+(π﹣1)0﹣(  )﹣1;
)﹣1;
(2)化简:(m+2)(m﹣2)﹣(2﹣m)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列问题:
(1)一项工程,甲队单独做需10天完成,乙队单独做需15天完成,甲先做5天后,甲、乙合作完成余下的工作,问两队合做几天可以完成这项工作?
(2)从A地到B地,甲需走10小时,从B地到A地,乙需走15小时,甲、乙两人从A,B两地相向而行,甲出发5小时后乙出发,问乙出发几小时后两人相遇?
(3)一笔钱款,可以买甲种商品10件或买乙种商品15件,用这笔钱款买了甲、乙两种商品,已知甲种商品比乙种商品多买了5件,问乙种商品买了几件?
(4)通过解答上面三个问题,你发现了什么?
(5)根据上面所列的方程,编写一道实际问题的应用题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

-
科目: 来源: 题型:
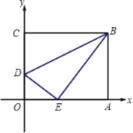
查看答案和解析>>【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
相关试题

