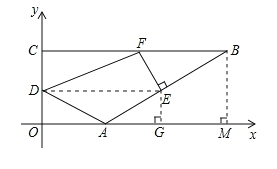
【题目】如图,在平面直角坐标系中,点A(![]() ,0),B(3
,0),B(3![]() ,2),C(0,2).动点D以每秒1个单位的速度
,2),C(0,2).动点D以每秒1个单位的速度
从点0出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF上AB,交BC于点F,连结DA、DF.设运动时间为t秒.
(1)求∠ABC的度数;
(2)当t为何值时,AB∥DF;
(3)设四边形AEFD的面积为S.
①求S关于t的函数关系式;
②若一抛物线y=x2+mx经过动点E,当S<2![]() 时,求m的取值范围(写出答案即可).
时,求m的取值范围(写出答案即可).

参考答案:
【答案】(1)30o;(2) ![]() ;(3)
;(3) ![]()
![]()
【解析】试题分析:(1)求∠ABC的度数即求∠BAx的度数,过B作BM⊥x轴于M,则AM=2![]() ,BM=2,由此可得出∠BAM即∠ABC的度数.
,BM=2,由此可得出∠BAM即∠ABC的度数.
(2)当AB∥FD时,∠CFD=∠B=30°,可在直角三角形CDF中,用CD的长表示出CF,同理可在直角三角形FEB中,用BE的长表示出BF,然后可根据CF+BF=BC来求出t的值.
(3)①连接DE,根据D、E的速度可知AE=2OD,而AE=2EG,因此OD∥=EG,即四边形ODEG是矩形,因此DE∥x轴,那么四边形AEFD的面积可分成三角形ADE和三角形EFD两部分来求出.两三角形都以DE为底,两三角形高的和正好是OC的长,因此四边形ADEF的面积就等于![]() DEOC,关键是求出DE的长.如果过A作DE的垂线不难得出DE=OA+AEsin60°,由此可得出S,t的函数关系式.
DEOC,关键是求出DE的长.如果过A作DE的垂线不难得出DE=OA+AEsin60°,由此可得出S,t的函数关系式.
②已知了S的取值范围可根据①的函数关系式求出t的取值范围.在①题已经求得了E点坐标,将其代入抛物线的解析式中,用m表示出t的值,然后根据t的取值范围即可求出m的取值范围.
试题解析:
(1)过点B作BM⊥x轴于点M
∵C(0,2),B(![]() )
)
∴BC∥OA
∴∠ABC=∠BAM
∵BM=2,AM=![]()
∴tan∠BAM=![]()
∴∠ABC=∠BAM=30°.
(2)∵AB∥DF
∴∠CFD=∠CBA=30°
在Rt△DCF中,CD=2-t,∠CFD=30°,
∴CF=![]() (2-t)
(2-t)
∴AB=4,
∴BE=4-2t,∠FBE=30°,
∴BF=![]()
∴![]()
∴t=![]()
(3)①连接DE,过点E作EG⊥x轴于点G,
则EG=t,OG=![]() t+
t+![]()
∴E(![]() t+
t+![]() ,t)
,t)
∴DE∥x轴
S=S△DEF+S△DEA=![]() DE×CD+
DE×CD+![]() DE×OD
DE×OD
=![]() t+
t+![]()
②当S<![]() 时,
时,
由①可知,S=![]() t+
t+![]()
∴![]() t+
t+![]() <
<![]()
∴t<1,
∵t>0,
∴0<t<1,
∵y=-x2+mx,点E(![]() t+
t+![]() ,t)
,t)
当t=0时,E(![]() ,0)
,0)
∴m=![]()
当t=1时,E(![]() ,1)
,1)
∴m=![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】深高北校区初二年级举行“名著知识竟赛”决赛.在这之前,初二(24)班举行了三轮初赛,为了从甲乙两名平均分最高的同学中选取一名发挥稳定的同学参加决赛,需要考察这两位同学三轮初赛成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解ax2-9a=.
-
科目: 来源: 题型:
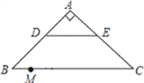
查看答案和解析>>【题目】如图,在Rt△ABC中.∠A=90°.AB=AC,BC=20,DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3a2﹣12= ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某学校初四年纪学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
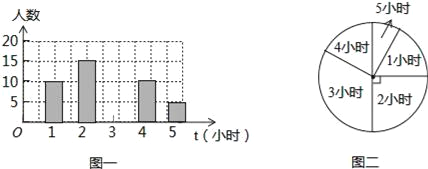
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打折.
相关试题

