【题目】为了了解某学校初四年纪学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
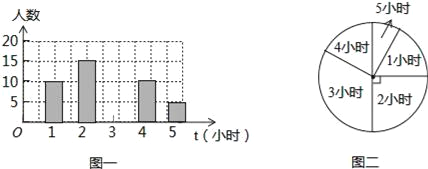
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
参考答案:
【答案】(1)①m=60;②30o;③见解析;(2)众数、中位数为5;平均数2.92.
【解析】试题分析:(1)①根据2小时所占扇形的圆心角的度数确定其所占的百分比,然后根据条形统计图中2小时的人数求得m的值;
②结合周角是360度进行计算;
③求得总人数后减去其他小组的人数即可求得第三小组的人数;
(2)利用众数、中位数的定义及平均数的计算公式确定即可.
试题解析:
(1)①∵课外阅读时间为2小时的所在扇形的圆心角的度数为90°,
∴其所占的百分比为![]() ,
,
∵课外阅读时间为2小时的有15人,
∴m=15÷![]() =60;
=60;
②5小时的扇形圆心角的度数: ![]() ,
,
③第三小组的频数为:60-10-15-10-5=20,
补全条形统计图为:
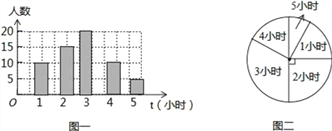
(2)∵课外阅读时间为3小时的20人,最多,
∴众数为 3小时;
∵共60人,中位数应该是第30和第31人的平均数,且第30和第31人阅读时间均为3小时,
∴中位数为3小时;平均数为: ![]() ≈2.92小时.
≈2.92小时.
-
科目: 来源: 题型:
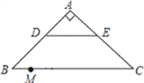
查看答案和解析>>【题目】如图,在Rt△ABC中.∠A=90°.AB=AC,BC=20,DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
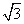 ,0),B(3
,0),B(3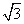 ,2),C(0,2).动点D以每秒1个单位的速度
,2),C(0,2).动点D以每秒1个单位的速度从点0出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF上AB,交BC于点F,连结DA、DF.设运动时间为t秒.
(1)求∠ABC的度数;
(2)当t为何值时,AB∥DF;
(3)设四边形AEFD的面积为S.
①求S关于t的函数关系式;
②若一抛物线y=x2+mx经过动点E,当S<2
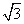 时,求m的取值范围(写出答案即可).
时,求m的取值范围(写出答案即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:3a2﹣12= ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打折.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
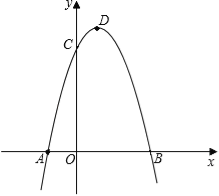
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判定两个直角三角形全等的是( )
A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
相关试题

