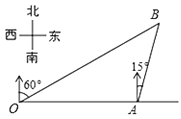
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测点O处测得该船位于北偏东60°的方向,则该船航行的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
根据题意,可以作辅助线AC⊥OB于点C,然后根据题目中的条件,可以求得AC和BC的长度,然后根据勾股定理即可求得AB的长.
作AC⊥OB于点C,如图所示,
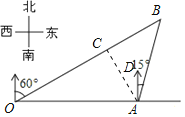
由已知可得,
∠COA=30°,OA=6km,
∵AC⊥OB,
∴∠OCA=∠BCA=90°,
∴OA=2AC,∠OAC=60°,
∴AC=3km,∠CAD=30°,
∵∠DAB=15°,
∴∠CAB=45°,
∴∠CAB=∠B=45°,
∴BC=AC,
∴AB=![]() (km),
(km),
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能完全地写出来,于是小明用
的小数部分我们不可能完全地写出来,于是小明用 ﹣1来表示
﹣1来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为 的整数部分是1,用这个数减去其整数部分,差就是小数部分.
的整数部分是1,用这个数减去其整数部分,差就是小数部分.请解答下列问题:
(1)求出
 +2的整数部分和小数部分;
+2的整数部分和小数部分;(2)已知:10+
 =x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数.
=x+y,其中x是整数,且0<y<1,请你求出(x﹣y)的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:① x + y=a;② x-y=b;③ a2-b2=2xy;④ x2-y2=ab;⑤ x2 + y2=
 ,其中正确的有__________.
,其中正确的有__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,如图为边长为a的大正方形中有一个边长为b的小正方形,如图是由如图中阴影部分拼成的一个长方形.

(1)设如图中阴影部分面积为S1,如图中阴影部分面积为S2,请用含a、b的代数式表示:
 ____ __,
____ __, ___ ___(只需表示,不必化简);
___ ___(只需表示,不必化简);(2)以上结果可以验证哪个乘法公式?
请写出这个乘法公式__ ____;
(3)利用(2)中得到的公式,
计算:
 .
. -
科目: 来源: 题型:
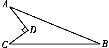
查看答案和解析>>【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块地,AD=8 m,CD=6 m,∠ADC=90°,AB=26 m,BC=24 m.求这块地的面积.
相关试题

