【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
参考答案:
【答案】解:∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠ACP=120°,
∵△ACP∽△PDB,
∴∠APC=∠B,又∠A=∠A,
∴△ACP∽△ABP,
∴∠APB=∠ACP=120°
【解析】由等边三角形的三个角都是60°易得∠ACP=120°,又由所给△ACP∽△PDB可证△ACP∽△ABP,最后可得∠APB=∠ACP=120°
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:① x + y=a;② x-y=b;③ a2-b2=2xy;④ x2-y2=ab;⑤ x2 + y2=
 ,其中正确的有__________.
,其中正确的有__________.
-
科目: 来源: 题型:
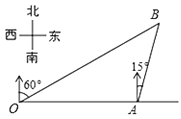
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测点O处测得该船位于北偏东60°的方向,则该船航行的距离为( )
A.
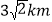 B.
B. 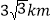 C.
C.  D.
D. 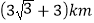
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,如图为边长为a的大正方形中有一个边长为b的小正方形,如图是由如图中阴影部分拼成的一个长方形.

(1)设如图中阴影部分面积为S1,如图中阴影部分面积为S2,请用含a、b的代数式表示:
 ____ __,
____ __, ___ ___(只需表示,不必化简);
___ ___(只需表示,不必化简);(2)以上结果可以验证哪个乘法公式?
请写出这个乘法公式__ ____;
(3)利用(2)中得到的公式,
计算:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块地,AD=8 m,CD=6 m,∠ADC=90°,AB=26 m,BC=24 m.求这块地的面积.
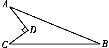
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
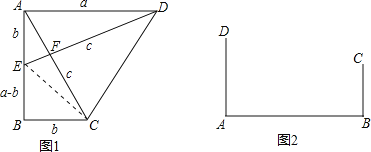
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式
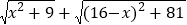 最小值(0<x<16)
最小值(0<x<16) -
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
一户居民一个月用电量的范围
电费价格(单位:元/度)
不超过200度
a
超过200度的部分
b
已知4月份,该市居民甲用电250度,交电费130元;居民乙用电400度,交电费220元.
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元?
相关试题

