【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案?
参考答案:
【答案】
(1)解:设排球单价为x元,则足球单价为(x+30)元,由题意得:
![]() =
= ![]() ,
,
解得:x=50,
经检验:x=50是原分式方程的解,
则x+30=80.
答:排球单价是50元,则足球单价是80元;
(2)解:设设恰好用完1200元,可购买排球m个和购买足球n个,
由题意得:50m+80n=1200,
整理得:m=24﹣ ![]() n,
n,
∵m、n都是正整数,
∴①n=5时,m=16,②n=10时,m=8;
∴有两种方案:
①购买排球5个,购买足球16个;
②购买排球10个,购买足球8个.
【解析】(1)设排球单价是x元,则足球单价是(x+30)元,根据题意可得等量关系:500元购得的排球数量=800元购得的足球数量,由等量关系可得方程,再求解即可;(2)设恰好用完1200元,可购买排球m个和购买足球n个,根据题意可得排球的单价×排球的个数m+足球的单价×足球的个数n=1200,再求出整数解即可得出答案.
【考点精析】通过灵活运用分式方程的应用,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+2x+3与x轴交于点A,B(A在B的左侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)抛物线的对称轴上存在点P,使∠APB=∠ABC,利用图1求点P的坐标;
(3)点Q在y轴右侧的抛物线上,利用图2比较∠OCQ与∠OCA的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得线段CD的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.

(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68. 频数分布表
分数段
频数(人数)
60≤x<70
a
70≤x<80
16
80≤x<90
24
90≤x<100
b

请解答下列问题:
(1)完成频数分布表,a= , b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;
(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论.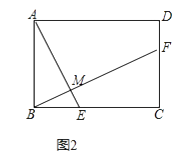
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l的解析式为y=﹣2x+2,分别交x轴、y轴于点A,B.

(1)写出A,B两点的坐标,并画出直线l的图象;
(2)将直线l向上平移4个单位得到l1 , l1交x轴于点C. ①作出l1的图象,
②l1的解析式是 .
(3)将直线l绕点A顺时针旋转90°得到l2 , l2交l1于点D. ①作出l2的图象,
②tan∠CAD= .
相关试题

