【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68. 频数分布表
分数段 | 频数(人数) |
60≤x<70 | a |
70≤x<80 | 16 |
80≤x<90 | 24 |
90≤x<100 | b |

请解答下列问题:
(1)完成频数分布表,a= , b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
参考答案:
【答案】
(1)4;4
(2)解:补全频数分布直方图如下:

(3)解:600× ![]() =50(人),
=50(人),
故答案为:估计该校成绩90≤x<100范围内的学生有50人.
(4)解:画树状图得:
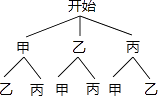
∵共有6种等可能的结果,甲、乙被选中的有2种情况,
∴甲、乙被选中的概率为 ![]() =
= ![]() .
.
【解析】解:(1)由题意知,60≤x<70的有60、63、67、68这4个数,90≤x<100的有90、99、99、99这4个, 即a=4、b=4,
所以答案是:4,4;
【考点精析】认真审题,首先需要了解频数分布直方图(特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图)),还要掌握列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得线段CD的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.

(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.
(1)排球和足球的单价各是多少元?
(2)若恰好用去1200元,有哪几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;
(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论.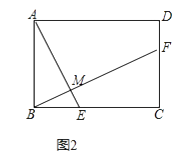
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l的解析式为y=﹣2x+2,分别交x轴、y轴于点A,B.

(1)写出A,B两点的坐标,并画出直线l的图象;
(2)将直线l向上平移4个单位得到l1 , l1交x轴于点C. ①作出l1的图象,
②l1的解析式是 .
(3)将直线l绕点A顺时针旋转90°得到l2 , l2交l1于点D. ①作出l2的图象,
②tan∠CAD= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.

A.20( +1)
+1)
B.20( ﹣1)
﹣1)
C.200
D.300
相关试题

