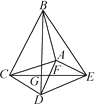
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S四边形BCDE=![]() BD·CE;⑤BC2+DE2=BE2+CD2.其中正确的结论有( )
BD·CE;⑤BC2+DE2=BE2+CD2.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
根据等腰直角三角形的性质可得AB=AC,AD=AE,然后求出∠BAD=∠CAE,再利用“边角边"证明△ABD和△ACE全等,根据全等三角形对应边相
等可得CE=BD,判断①正确;根据全等三角形对
应角相等可得∠ABD=∠ACE,从而求出∠BCG+∠CBG=∠ACB+∠ABC=90°,再求出∠BGC=90°,从而得到BD⊥CE,根据四边形的面积判断出
④正确;根据勾股定理表示出![]() ,得到⑤正确;再求出AE∥CD时,∠ADC=90°,判断出②错误;∠AEC与∠BAE不一定相等判断出③错误.
,得到⑤正确;再求出AE∥CD时,∠ADC=90°,判断出②错误;∠AEC与∠BAE不一定相等判断出③错误.
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC, AD=AE,
∴∠BAD=∠BAC+∠CAD=90°+∠CAD,
∠CAE=∠DAE+∠CAD=90+∠CAD
∴∠BAD=∠CAE
在△ABD和△ACE中,
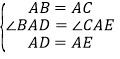
∴△ABD≌△ACE(SAB),
∴CE=BD,①正确;
∠ABD=∠ACF
∠BCG+∠CBG=∠ACB+∠ABC=90°,
在△BCG中,∠BGC=180°-(∠BCG+∠CBG)
=180°- 90°=90°
∴BD⊥CE,
∴四边形ABCD的面积=![]() 故④正确;
故④正确;
由勾股定理,在Rt△BCG中![]()
由勾股定理,在Rt△DEG中,![]()
∴![]()
在Rt△BGE中,![]()
在Rt△CDG中,![]()
∴![]()
∴![]()
故⑤正确;
只有AE∥CD时,∠AEC=∠DCE,
∠ADC=∠ADB+∠BDC=90°
无法说明AE∥CD,故②错误;
∵△ABD≌△ACE
∴∠ADB=∠AEC
∵∠AEC与∠AEB相等无法证明,
∴∠ADB=∠AEB不一定成立,故③错误;
综上所述,正的结论有①④⑤共3个.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=
 ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )A. 1个; B. 2个; C. 3个; D. 4个;
-
科目: 来源: 题型:
查看答案和解析>>【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,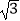 =1.732,
=1.732, 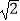 =1.414)
=1.414)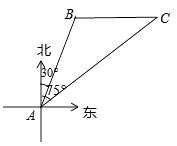
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
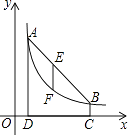
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF= AD,求出点E的坐标.
AD,求出点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.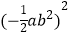 =
=  ab4
ab4
B.(﹣1+b)(﹣b﹣1)=1﹣b2
C.5xy2﹣xy2=4
D.(a﹣b)2=a2+b2
相关试题

