【题目】如图,直线y= ![]() x﹣
x﹣ ![]() 与x,y轴分别交于点A,B,与反比例函数y=
与x,y轴分别交于点A,B,与反比例函数y= ![]() (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(1)求点A的坐标.
(2)若AE=AC.
①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由.
参考答案:
【答案】
(1)
解:当y=0时,得0= ![]() x﹣
x﹣ ![]() ,解得:x=3.
,解得:x=3.
∴点A的坐标为(3,0)
(2)
解:①过点C作CF⊥x轴于点F,如图所示.
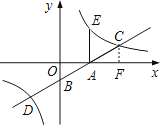
设AE=AC=t,点E的坐标是(3,t),
在Rt△AOB中,tan∠OAB= ![]() =
= ![]() ,
,
∴∠OAB=30°.
在Rt△ACF中,∠CAF=30°,
∴CF= ![]() t,AF=ACcos30°=
t,AF=ACcos30°= ![]() t,
t,
∴点C的坐标是(3+ ![]() t,
t, ![]() t).
t).
∴(3+ ![]() t)×
t)× ![]() t=3t,
t=3t,
解得:t1=0(舍去),t2=2 ![]() .
.
∴k=3t=6 ![]() .
.
②点E与点D关于原点O成中心对称,理由如下:
设点D的坐标是(x, ![]() x﹣
x﹣ ![]() ),
),
∴x( ![]() x﹣
x﹣ ![]() )=6
)=6 ![]() ,解得:x1=6,x2=﹣3,
,解得:x1=6,x2=﹣3,
∴点D的坐标是(﹣3,﹣2 ![]() ).
).
又∵点E的坐标为(3,2 ![]() ),
),
∴点E与点D关于原点O成中心对称
【解析】(1)令一次函数中y=0,解关于x的一元一次方程,即可得出结论;(2)①过点C作CF⊥x轴于点F,设AE=AC=t,由此表示出点E的坐标,利用特殊角的三角形函数值,通过计算可得出点C的坐标,再根据反比例函数图象上点的坐标特征可得出关于t的一元二次方程,解方程即可得出结论;
②根据点在直线上设出点D的坐标,根据反比例函数图象上点的坐标特征可得出关于点D横坐标的一元二次方程,解方程即可得出点D的坐标,结合①中点E的坐标即可得出结论.本题考查了反比例函数与一次函数的交点问题、解一元二次方程以及反比例函数图象上点的坐标特征,解题的关键是:(1)令一次函数中y=0求出x的值;(2)根据反比例函数图象上点的坐标特征得出一元二次方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数图象上点的坐标特征找出关于点的横坐标的一元二次方程是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级某班级部分同学去植树,若每人平均植树7棵,还剩9棵,若每人平均植树9棵,则有1位同学植树的棵数不到8棵.若设同学人数为x人,植树的棵数为(7x+9)棵,下列各项能准确的求出同学人数与种植的树木的数量的是( )
A. 7x+9≤8+9(x﹣1) B. 7x+9≥9(x﹣1)
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.

(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).北京时间
7:30
11:15
2:50
首尔时间
8:30
12:15
3:50
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
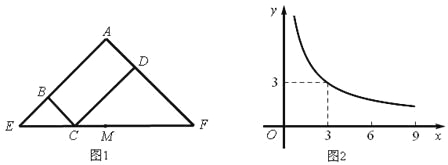
A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景点的门票价格如表:
购票人数/人
1~50
51~100
100以上
每人门票价/元
12
10
8
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
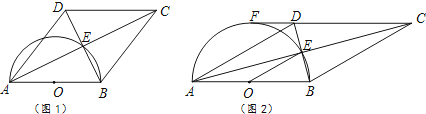
(1)利用图1,求证:四边形ABCD是菱形.
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长.
相关试题

