【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
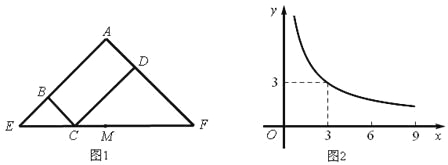
A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
参考答案:
【答案】B
【解析】试题分析:由图象可知,反比例函数图象经过(3,3),应用待定系数法可得该反比例函数关系式为![]() ,因此,
,因此,
当x=3时,y=3,点C与点M重合,即EC=EM,选项A错误;
根据等腰直角三角形的性质,当x=3时,y=3,点C与点M重合时,EM=![]() , 当y=9时,
, 当y=9时, ![]() ,即EC=
,即EC=![]() ,所以,EC<EM,选项B错误;
,所以,EC<EM,选项B错误;
根据等腰直角三角形的性质,EC= ![]() ,CF=
,CF= ![]() , 即EC·CF=
, 即EC·CF=![]() ,为定值,所以不论x如何变化,EC·CF的值不变,选项C错误;
,为定值,所以不论x如何变化,EC·CF的值不变,选项C错误;
根据等腰直角三角形的性质,BE=x,DF=y,所以BE·DF= ![]() ,为定值,所以不论y如何变化,BE·DF的值不变,选项D正确.
,为定值,所以不论y如何变化,BE·DF的值不变,选项D正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.

(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).北京时间
7:30
11:15
2:50
首尔时间
8:30
12:15
3:50
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
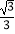 x﹣
x﹣  与x,y轴分别交于点A,B,与反比例函数y=
与x,y轴分别交于点A,B,与反比例函数y= 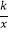 (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
(1)求点A的坐标.
(2)若AE=AC.
①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某景点的门票价格如表:
购票人数/人
1~50
51~100
100以上
每人门票价/元
12
10
8
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
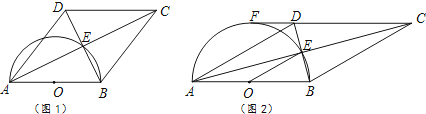
(1)利用图1,求证:四边形ABCD是菱形.
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.

(1)如图2,若α=60°,OE=OA,求直线EF的函数表达式.
(2)若α为锐角,tanα= ,当AE取得最小值时,求正方形OEFG的面积.
,当AE取得最小值时,求正方形OEFG的面积.
(3)当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为 :1?若能,求点P的坐标;若不能,试说明理由
:1?若能,求点P的坐标;若不能,试说明理由
相关试题

