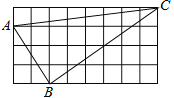
【题目】如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
(1)求△ABC的面积;
(2)判断△ABC是什么形状? 并说明理由.
参考答案:
【答案】(1)13;(2)网格中的△ABC是直角三角形.
【解析】(1)用长方形的面积减去三个小三角形的面积即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而不难得到其形状.
解:(1)△ABC 的面积=4 ×8-1 ×8 ÷2-2 ×3 ÷2-6 ×4 ÷2=13
故△ABC 的面积为13;
(2)∵正方形小方格边长为1
∴AC=![]() ,
,![]() ,
,![]()
∵在△ABC 中,AB2+BC2=13+52=65 ,AC2=65,
∴AB2+BC2=AC2,
∴网格中的△ABC是直角三角形.
“点睛”考查了三角形的面积,勾股定理和勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于平方根,下列说法正确的是( )
A. 任何一个数都有两个平方根,并且它们互为相反数 B. 负数没有平方根
C. 任何一个数都只有一个算术平方根 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣
 x+1与y轴交于点D.
x+1与y轴交于点D.(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,同弦所对的圆周角( )
A.相等
B.互补
C.相等或互补
D.都不对 -
科目: 来源: 题型:
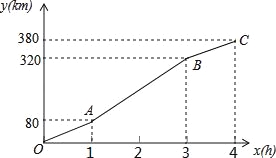
查看答案和解析>>【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图4所示.

(1)根据图示填写下表:
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A. 25 B. 14 C. 7 D. 7或25
相关试题

