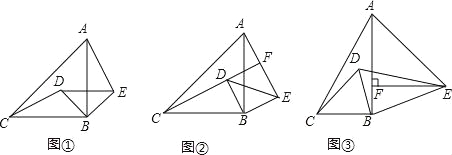
【题目】阅读发现:(1)如图①,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,AB=BC=3,BD=BE=1,连结CD,AE.易证:△BCD≌△BAE.(不需要证明)
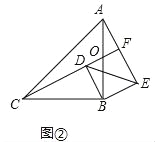
提出问题:(2)在(1)的条件下,当BD∥AE时,延长CD交AE于点F,如图②,求AF的长.
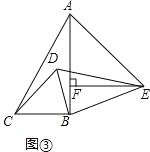
解决问题:(3)如图③,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠BAC=∠DEB=30°,连结CD,AE.当∠BAE=45°时,点E到AB的距离EF的长为2,求线段CD的长为 .
参考答案:
【答案】(2)AF=2![]() ﹣1;
﹣1;
(3)![]() .
.
【解析】
试题分析:(2)由△BCD≌△BAE,得到∠OAF=∠OCB,根据“8字型”证明∠AFO=∠CBO=90°,在RT△BDC中利用勾股定理求出CD,再证明BD=EF即可解决问题.
(3)根据两边成比例夹角相等两三角形相似,可以证明△ABE∽△CBD,得![]() ,再求出AE即可解决问题.
,再求出AE即可解决问题.
试题解析:(2)如图②中,AB与CF交于点O.
由(1)可知:△BCD≌△BAE,
∴∠OAF=∠OCB,CD=AE,∵∠AOF=∠COB,
∴∠AFO=∠CBO=90°,
∴CF⊥AE,∵BD∥AE,
∴BD⊥CF,
在RT△CDB中,∵∠CDB=90°,BC=3,BD=1,
∴CD=AE=![]() =2
=2![]() ,
,
∵∠BDF=∠DFE=∠DBE=90°,
∴四边形EFDB是矩形,
∴EF=BD=1,
∴AF=AE﹣EF=2![]() ﹣1.
﹣1.
(3)在RT△ABC,RT△EBD中,∵∠ABC=∠DBE=90°,∠BAC=∠DEB=30°,
∴AB=![]() BC,BE=
BC,BE=![]() BD,
BD,
∴![]() ,
,
∵∠ABC=∠EBD=90°,
∴∠ABE=∠DBC,
∴△ABE∽△CBD,
∴![]() ,
,
在RT△AEF中,∵∠AFE=90°,∠EAF=45°,EF=2,
∴AF=EF=2,AE=2![]() ,
,
∴![]() ,
,
∴CD=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2 cm变成5 cm时,圆形的面积从_____变成________.这一变化过程中_______是自变量,_______是自变量的函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ab2﹣a3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】据《经济日报》报道,某市2019年累计接待游客1362万人次,旅游总收入达75亿元.同比增幅双双超过30%,其中数据1362万用科学记数法表示为___________________人次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( ) ①4x+8=0变形为x+2=0;
②x+6=5﹣2x变形为3x=﹣1;
③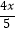 =3变形为4x=15;
=3变形为4x=15;
④4x=2变形为x=2.
A.①④
B.①②③
C.③④
D.①②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】李钰同学利用计算机设计了一个程序,输入和输出的数据如下表:
输入
…
1
2
3
4
5
…
输出
…
2
5
10
17
26
…
那么,当输入数据8时,输出的数据是( )
A. 61 B. 63 C. 65 D. 67
相关试题

