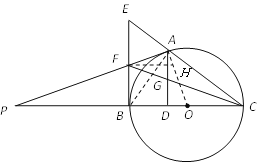
【题目】如图1,BC是⊙O的直径,A是⊙O上一点,过点B作⊙O的切线,与CA的延长线相交于点E,F是BE的中点,延长AF与CB的延长线相交于点P.
(1)求证:PA是⊙O的切线;
(2)如图2,若AD⊥BC于点D,连接CF与AD相交于点G.求证:AG=GD;
(3)在(2)的条件下,若FG=BF,且⊙O的半径长为![]() ,求BD的长度.
,求BD的长度.

参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)BD的长度为![]()
【解析】试题分析:(1)根据切线判定知道EB⊥BC,而AD⊥BC,从而可以确定AD∥BE,那么△BFC∽△DGC,又G是AD的中点,就可得出结论BF=EF.(2)要证PA是 O的切线,就是要证明∠PAO=90°连接AO,AB,根据第1的结论和BE是 O的切线和直角三角形的等量代换,就可得出结论.(3)点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性和勾股定理,可以求出BD和FG的长度.
试题解析:(1)证明:连结![]() .
.
![]() 是⊙O的直径,
是⊙O的直径, ![]() .
.
在![]() 中,因为
中,因为![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() .
. ![]() .
.
又![]() ,
, ![]() .
.
![]() 是⊙O的切线,
是⊙O的切线, ![]() .
.
![]() ,
,
![]() 是⊙O的切线.
是⊙O的切线.
(2)证明: ![]()
又![]() ,
, ![]() .
.
易证![]() ,
, ![]() .
.
![]()
![]() .
.
∵BF=EF
![]() .
.
(3)解:过点![]() 作
作![]() 于点
于点![]() .
.
![]() 四边形
四边形![]() 是矩形,
是矩形, ![]() .
.
由(1),∵BE=AF=FE.
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
∵四边形![]() 是矩形,
是矩形,
∴FH∥BC
![]()
![]()
∴![]() .
.
∵![]() ,
,
∴CF=3FG.
在Rt△FBC中,
∵CF=3FG,BF=FG,
∴CF2=BF2+BC2∴(3FG)2=FG2+(6![]() )2
)2
解得FG=3(负值舍去)
∴FG=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角为75°,则它的余角的度数为( )
A.285°
B.105°
C.75°
D.15° -
科目: 来源: 题型:
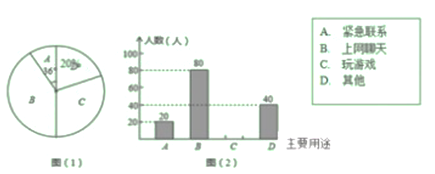
查看答案和解析>>【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,随机抽查了某中学九年级的同学,关于手机在中学生中的主要用途做了调查,对调查数据进行统计整理、制作了如下的两种统计图:请根据图形回答问题
(1)这次被调查的学生共有______人,其中主要用于“上网聊天”的学生人数占抽样人数的百分比为_____;
(2)请你将条形统计图(2)补充完整;
(3)若该校共有3000名学生,请你估计主要使用手机玩游戏的人数大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图. 根据以上信息,解答下列问题:
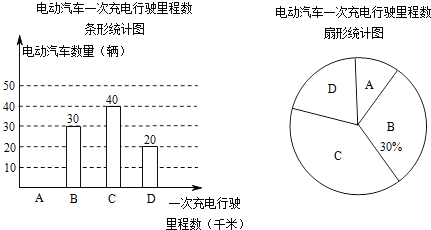
(1)问这次被抽检的电动汽车共有几辆?
(2)补全条形统计图,并求出C等级对应的圆心角度数.
(3)估计这种电动汽车一次充电后行驶的平均里程数为多少千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式x2-mx+n与x-2的乘积中不含x2项和x项,试求m和n的值,并求这两个多项式的乘积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】b和2的比例中项是4,则b=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是一元二次方程(m﹣2)x2+(m2﹣3)x﹣m+1=0的一根,则m=__.
相关试题

