【题目】如图,平移线段AB,使点A移动到点A1.
(1)画出平移后的线段A1B1,分别连接AA1,BB1.
(2)分别画出AC⊥A1B1于点C,AD⊥BB1于点D.
(3)AA1与BB1之间的距离,就是线段 的长度.
(4)线段AB平移的距离,就是线段 的长度.
(5)线段BD的长度,是点B到直线 的距离.

参考答案:
【答案】(1)见解析(2)见解析(3)AD(4)AA1(5)AD
【解析】
(1)连接AA1,再过B作BB1平行且等于AA1,再连接A1B1即可;
(2)利用直角三角板过A作AC⊥A1B1,过A作AD⊥BB1即可;
(3)AD长度就是AA1与BB1之间的距离;
(4)线段AB平移的距离,就是线段AA1或BB1的长;
(5)根据点到直线的距离就是垂线段的长度可得答案.
(1)如图所示;
(2)如图所示;
(3)AA1与BB1之间的距离,就是线段AD的长度.
故答案为:AD;
(4)线段AB平移的距离,就是线段AA1的长度.
故答案为:AA1;
(5)线段BD的长度,是点B到直线AD的距离.
故答案为:AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)(﹣ab)3(5a2b﹣4ab2);
(2)(2x﹣1)(4x2+2x+1)
(3)求5x(2x+1)﹣(2x+3)(5x﹣1)的值,其中x=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组:
(1)
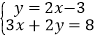
(2)
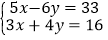
(3)
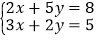
-
科目: 来源: 题型:
查看答案和解析>>【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场
乙林场
购树苗数量
销售单价
购树苗数量
销售单价
不超过1000棵时
4元/棵
不超过2000棵时
4元/棵
超过1000棵的部分
3.8元/棵
超过2000棵的部分
3.6元/棵
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为元,若都在乙林场购买所需费用为元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列推理过程,将空白部分补充完整.
(1)如图1,∠ABC=∠A1B1C1,BD,B1D1分别是∠ABC,∠A1B1C1的角平分线,对∠DBC=∠D1B1C1进行说理.
理由:因为BD,B1D1分别是∠ABC,∠A1B1C1的角平分线
所以∠DBC= ,∠D1B1C1= (角平分线的定义)
又因为∠ABC=∠A1B1C1
所以
 ∠ABC=
∠ABC= ∠A1B1C1
∠A1B1C1所以∠DBC=∠D1B1C1( )

(2)如图2,EF∥AD,∠1=∠2,∠B=40°,求∠CDG的度数.
因为EF∥AD,
所以∠2= ( )
又因为∠1=∠2 (已知)
所以∠1= (等量代换)
所以AB∥GD( )
所以∠B= ( )
因为∠B=40°(已知)
所以∠CDG= (等量代换)
(3)下面是“积的乘方的法则“的推导过程,在括号里写出每一步的依据.
因为(ab)n=
 ( )
( )=
 ( )
( )=anbn( )
所以(ab)n=anbn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
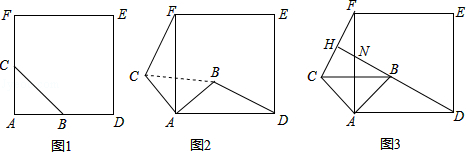
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3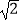 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数:
﹣3.1,3.1415,﹣
 ,+31,0.618,﹣
,+31,0.618,﹣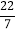 ,0,﹣1,﹣(﹣3),填在相应的集合里
,0,﹣1,﹣(﹣3),填在相应的集合里分数集合: ;
整数集合: ;
非负整数集合: ;
正有理数集合: .
相关试题

