【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数![]() 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(
;(3)E(![]() ,
,![]() ).
).
【解析】
试题分析:(1)把点A(3,3)代入![]() 中,得:3=9+3b,解得:b=﹣2,∴二次函数的表达式为
中,得:3=9+3b,解得:b=﹣2,∴二次函数的表达式为![]() .
.
(2)设点P在点Q的左下方,过点P作PE⊥QQ1于点E,如图1所示.
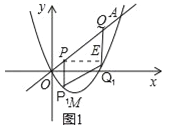
∵PE⊥QQ1,QQ1⊥x轴,∴PE∥x轴,∵直线OA的解析式为y=kx,∴∠QPE=45°,∴PE=![]() PQ=2.
PQ=2.
设点P(m,m)(0<m<1),则Q(m+2,m+2),P1(m,![]() ),Q1(m+2,
),Q1(m+2,![]() ),∴PP1=
),∴PP1=![]() ,QQ1=
,QQ1=![]() ,∴
,∴![]() =
=![]() (PP1+QQ1)PE=
(PP1+QQ1)PE=![]() =
=![]() ,∴当m=
,∴当m=![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]() .
.
(3)存在.
如图2中,点E的对称点为F,EF与AM交于点G,连接OM、MF、AF、OF.
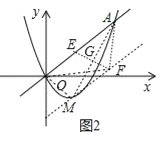
∵S△AOF=S△AOM,∴MF∥OA,∵EG=GF,![]() ,∴AG=GM,∵M(1,﹣1),A(3,3),∴点G(2,1),∵直线AM解析式为y=2x﹣3,∴线段AM的中垂线EF的解析式为
,∴AG=GM,∵M(1,﹣1),A(3,3),∴点G(2,1),∵直线AM解析式为y=2x﹣3,∴线段AM的中垂线EF的解析式为![]() ,由
,由 ,解得
,解得![]() ,∴点E坐标为(
,∴点E坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=2,b=﹣1,则a+2b+3的值为( )
A.﹣1
B.3
C.6
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A.随意翻到一本书的某页,页码是奇数
B.抛掷一枚普通硬币,正面朝下
C.抛得一枚普通正方体般子所得点数大于3
D.太阳每天从东方升起
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李到农贸批发市场了解到苹果和西瓜的价格信息如下:
水果品种
苹果
西瓜
批发价格
8元/公斤
1.6元/公斤
零售价格
10元/公斤
2元/公斤
他共用280元批发了苹果和西瓜共75公斤,
(1)请问小李批发的苹果和西瓜各多少公斤?
(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱? -
科目: 来源: 题型:
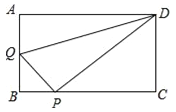
查看答案和解析>>【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
-
科目: 来源: 题型:
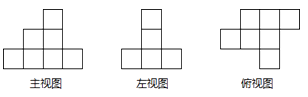
查看答案和解析>>【题目】如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a+2b=5ab B. 5a﹣2a=3a C. b2b3=b6 D. (x+y)2=x2+y2
相关试题

