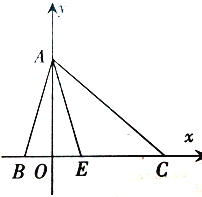
【题目】如图,点B,E关于y轴对称,且E在AC的垂直平分线上,已知点C(5,0).
(1)如果∠BAE=40°,那么∠C= °;
(2)如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长= cm;
(3)AB+BO= .
参考答案:
【答案】(1)35;(2)7;(3)5.
【解析】试题分析:
(1) 根据轴对称的性质可知,△ABE是等腰三角形. 根据三角形的内角和,容易得到∠AEB的度数. 根据线段垂直平分线的相关结论,可以得到∠C=∠CAE. 通过三角形外角的相关结论,不难求得∠C的度数.
(2) 根据线段垂直平分线的相关结论可知AE=EC. 因此,△ABE的周长为AB+BC. 由△ABC的周长和边AC的长,不难求得AB+BC的长,进而得到△ABE的周长.
(3) 根据前两个小题的解题过程可知,AB=AE,AE=EC. 由轴对称的性质可得BO=EO. 结合上述两个条件可知,AB+BO=EC+EO=OC. 由于线段OC的长代表了点C的横坐标值,所以利用点C的坐标即可得到AB+BO的值.
试题解析:
(1) ∵点B与点E关于y轴对称,
∴BO=EO,AO⊥BE,
∴AB=AE.
∵∠BAE=40°,AB=AE,
∴在△ABE中,![]() .
.
∵点E在AC的垂直平分线上,
∴AE=EC,
∴∠C=∠CAE.
∵∠AEB是△AEC的一个外角,
∴∠AEB=∠C+∠CAE=2∠C=70°,
∴∠C=35°.
故本小题应填写:35.
(2) ∵△ABC的周长为13cm,
∴AB+BC+AC=13cm,
∵AC=6cm,
∴AB+BC=13-6=7(cm).
∵△ABE的周长为AB+BE+AE,
又∵AE=EC,
∴AB+BE+AE=AB+BE+EC=AB+BC.
∴△ABE的周长为7cm.
故本小题应填写:7.
(3) ∵AB=AE,AE=EC,
∴AB=EC.
∵BO=EO,
∴AB+BO=EC+EO=OC.
∵点C的坐标为(5, 0),
∴OC=5.
故本小题应填写:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(﹣3,b)在第三象限内,则b( )
A. 是正数 B. 是负数
C. 是0 D. 可以是正数,也可以是负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点A(2,﹣3)和点B关于原点对称,则点B的坐标为( )
A. (﹣2,3) B. (﹣2,﹣3) C. (2,﹣3) D. (2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC=
 .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= .
.
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),已知AF平分∠BAC,交边BC于点E,过F作FD⊥BC,若∠B=x°,∠C=(x+36)°,
①∠CAE= (含x的代数式表示)
②求∠F的度数.
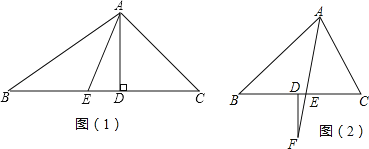
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2m、宽为2n的长方形,沿图中实线用剪刀均分成四块小长方形然后按图b的形状拼成一个大正方形.
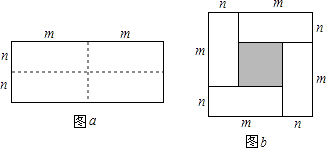
(1)图b中的小正方形的边长等于;
(2)图a中四个长方形的面积和为;图b中四个小长方形的面积和还可以表示为 .
(3)由(2)写出代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系:;
(4)根据(3)中的等量关系,解决如下问题:若x+y=8,xy=7,则(2x﹣2y)2= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个等腰三角形的两边长分别是5cm和6cm,那么此三角形的周长是
A.15cm B.16cm C.17cm D.16cm或17cm
相关试题

