【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. A,B之间D. B,C之间
参考答案:
【答案】A
【解析】
此题为数学知识的应用,由题意设一个停靠点,为使所有的人步行到停靠点的路程之和最小,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.
解:①以点A为停靠点,则所有人的路程的和=15×100+10×300=4500(米),
②以点B为停靠点,则所有人的路程的和=30×100+10×200=5000(米),
③以点C为停靠点,则所有人的路程的和=30×300+15×200=12000(米),
④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<100),则所有人的路程的和是:30m+15(100﹣m)+10(300﹣m)=4500+5m>4500,
⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<200),则总路程为30(100+n)+15n+10(200﹣n)=5000+35n>4500.
∴该停靠点的位置应设在点A;
故选:A.
-
科目: 来源: 题型:
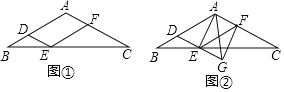
查看答案和解析>>【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分) 2011年5月上旬,无锡市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根
据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D
表示)四个等级进行统计,并绘制成如图所示的扇形图和统计表:
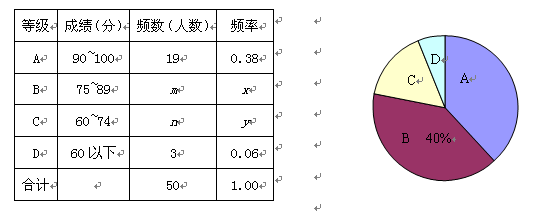
请你根据以上图表提供的信息,解答下列问题:
【1】(1) m= ,n= ,x= ,y= ;
【2】(2)在扇形图中,C等级所对应的圆心角是 度;
【3】(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
-
科目: 来源: 题型:
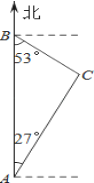
查看答案和解析>>【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈
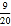 , cos27°≈
, cos27°≈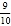 , tan27°≈
, tan27°≈ , sin53°≈
, sin53°≈ , cos53°≈
, cos53°≈ , tan53°≈
, tan53°≈ )
)
-
科目: 来源: 题型:
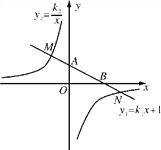
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y1=k1x+1的图象与y轴交于点A,与x轴交于点B,与反比例y2=
 象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.
象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时,x取值范围.
-
科目: 来源: 题型:
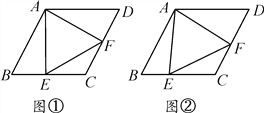
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解本校七年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对七年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中中度近视人数是不近视与重度近视人数之和的一半.
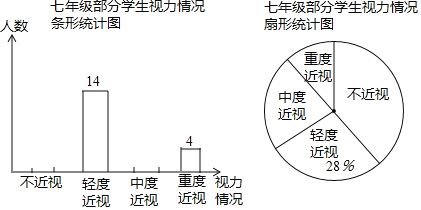
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图.在扇形统计图中,求“中度近视”对应扇形的圆心角的度数;
(3)若该校七年级学生有1200人,请你估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人?
相关试题

