【题目】某校为了了解本校七年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对七年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中中度近视人数是不近视与重度近视人数之和的一半.
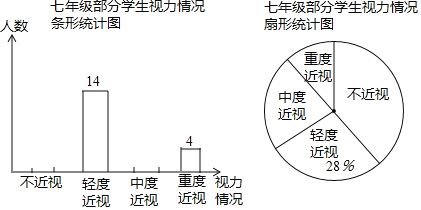
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图.在扇形统计图中,求“中度近视”对应扇形的圆心角的度数;
(3)若该校七年级学生有1200人,请你估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人?
参考答案:
【答案】(1)50(人);(2)图见解析,86.4°;(3)720
【解析】
(1)根据轻度近视的人数是14人,占总人数的28%,即可求得总人数;
(2)设中度近视的人数是x人,则不近视与重度近视人数的和为2x,列方程求得x的值,即可求得不近视的人数,然后利用360°乘以对应的百分比即可求得圆心角的度数;
(3)利用总人数乘以对应的百分比即可求解.
解:(1)本次调查的学生人数为14÷28%=50(人);
(2)设中度近视的人数是x人,则不近视与重度近视人数的和为2x,则x+2x+14=50,
解得:x=12,
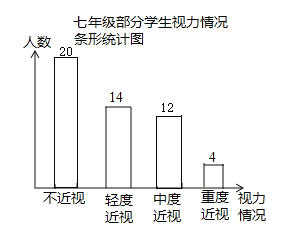
则中度近视的人数是12,不近视的人数是:24﹣4=20(人),
所以“中度近视”对应扇形的圆心角度数是:360°×![]() =86.4°;
=86.4°;
补全条形图如下:
(3)估计该校七年级近视(包括轻度近视,中度近视,重度近视)的学生大约有
1200×![]() =720(人).
=720(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
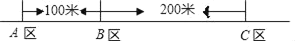
A. 点AB. 点BC. A,B之间D. B,C之间
-
科目: 来源: 题型:
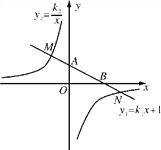
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y1=k1x+1的图象与y轴交于点A,与x轴交于点B,与反比例y2=
 象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.
象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时,x取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
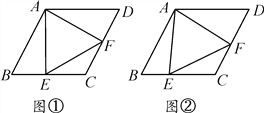
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校进行校园美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,如果由甲队先做20天,剩下的工程由甲、乙合作24天完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需要支付工程款3.5万元,乙队施工一天需要支付工程款2万元:如果规定在70天内完成这项工作,是由甲、乙两队单独完成省钱?还是由甲乙合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的三点A、B、C分别表示有理数a、b、c,且|a|>|c|>|b|.
(1)化简|a+c|﹣2|c﹣b|;
(2)若b的倒数是它本身,且AB:BO:OC=6:2:3,求(1)中代数式的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

相关试题

