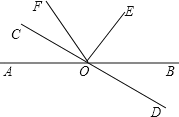
【题目】如图,直线![]() 、
、![]() 相交于
相交于![]() ,∠EOC=90°,
,∠EOC=90°,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,求
,求![]() 的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.
解:∵![]()
![]() ( )
( )
∴![]()
![]()
∵![]() 是
是![]() 的角平分线
的角平分线
∴![]()
![]() ( )
( )
∴![]()
![]()
∵![]()
![]()
![]() ( )
( )
∴![]()
![]() ( )
( )
参考答案:
【答案】已知,56,∠EOF,角平分线的定义,22,∠EOB,平角的定义,22,同角的余角相等.
【解析】
利用角的和差得出∠EOF的度数,利用角平分线的定义得到∠AOF的度数,进而得到∠AOC的度数,根据平角的定义和余角的性质即可得出结论.
∵![]()
![]() ( 已知 )
( 已知 )
∴![]() 56
56 ![]()
∵![]() 是
是![]() 的角平分线
的角平分线
∴![]() ∠EOF
∠EOF ![]() ( 角平分线的定义 )
( 角平分线的定义 )
∴![]() 22
22 ![]()
∵![]() ∠EOB
∠EOB ![]()
![]() ( 平角的定义 )
( 平角的定义 )
∴![]() 22
22 ![]() ( 同角的余角相等 ).
( 同角的余角相等 ).
故答案为:已知,56,∠EOF,角平分线的定义,22,∠EOB,平角的定义,22,同角的余角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点
 分别对应数
分别对应数 ,其中
,其中 .
.
 当
当 时,线段
时,线段 的中点对应的数是_ _____ .(直接填结果)
的中点对应的数是_ _____ .(直接填结果) 若该数轴上另有一点
若该数轴上另有一点 对应着数
对应着数 .
.①当
 ,且
,且 时,求代数式
时,求代数式 的值:
的值:②
 .且
.且 时学生小朋通过演算发现代数式
时学生小朋通过演算发现代数式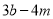 是一个定值
是一个定值老师点评:小朋同学的演算发现还不完整!
请你通过演算解释为什么“小朋的演算发现”是不完整的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y关于x的二次函数y=ax2﹣bx+2(a≠0).
(1)当a=﹣2,b=﹣4时,求该函数图象的对称轴及顶点坐标.
(2)在(1)的条件下,Q(m,t)为该函数图象上的一点,若Q关于原点的对称点P也落在该函数图象上,求m的值.
(3)当该函数图象经过点(1,0)时,若A(
 ,y1),B(
,y1),B( ,y2)是该函数图象上的两点,试比较y1与y2的大小.
,y2)是该函数图象上的两点,试比较y1与y2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“
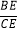 =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是北京怀柔医院一位病人在4月8日6时到4月10日18时的体温记录示意图,下列说法中,错误的是
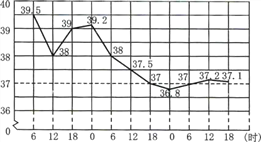
①护士每隔6小时给病人量一次体温;
②这个病人的体温最高是39.5摄氏度,最低36.8摄氏度;
③他的体温在4月9日18时到4月10日18时比较稳定;
④他的体温在4月8日18时到4月9日18时下降最快.
A. ① B. ②④ C. ④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在150≤x<175范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
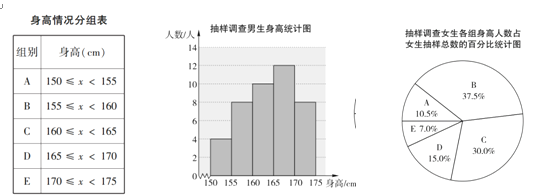
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高在155≤x<165之间的学生有18人;
②初一学生中女生的身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④初一学生身高在160≤x<170之间的学生约有800人.
其中合理的是
A. ①② B. ①④ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
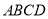 中,
中,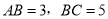 ,在
,在 上任取一点
上任取一点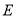 ,连接
,连接 .将
.将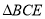 沿
沿 折叠,使点
折叠,使点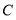 恰好落在
恰好落在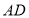 边上的点
边上的点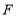 处,则
处,则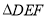 的面积为_______.
的面积为_______.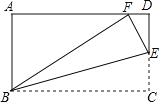
相关试题

