【题目】已知∠α和∠β互为补角,且∠β比∠α小20°,则∠β等于_____.
参考答案:
【答案】80°.
【解析】
根据∠α与∠β互为补角,可得∠α+∠β=180°,再根据∠β比∠α小20°,可得∠β=∠α-20,再进行等量代换可计算出∠α,进而得出∠β的度数.
解:∵∠α与∠β互为补角,
∴∠α+∠β=180°,
∵∠β比∠α小20°,
∴∠β=∠α-20°,
∴∠α+∠α-20°=180°,
解得∠α=100°,
∴∠β=100°-20°=80°.
故答案为:80°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知tan∠A=1,则锐角A=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣4=
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和与外角和之和是1800°,则此多边形是( )
A. 八边形 B. 十边形 C. 十二边形 D. 十四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.
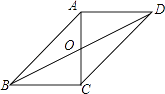
求:
(1)AC的长;
(2)求OB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是
 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.

-
科目: 来源: 题型:
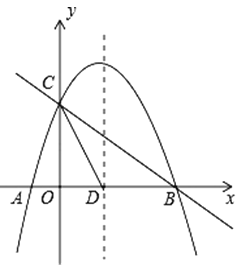
查看答案和解析>>【题目】如图,已知抛物线
 与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
相关试题

