搜索
【题目】在ABCD中，点O是对角线AC、BD的交点，AC垂直于BC，且AB=10cm，AD=8cm．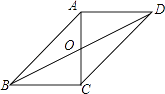 
求：
（1）AC的长；
（2）求OB的长．
参考答案：
【答案】
（1）解：在ABCD中BC=AD=8cm，
∵AC垂直于BC，
∴∠ACB=90°，
∴AC= 
=6cm
（2）解：∵OC= 
AC=3cm，
∴OB= 
= 
【解析】根据平行四边形的性质得到BC=AD=8cm，根据勾股定理即可得到结论．
【考点精析】根据题目的已知条件，利用勾股定理的概念和平行四边形的性质的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：a2﹣4=
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个多边形的内角和与外角和之和是1800°,则此多边形是( )
A. 八边形 B. 十边形 C. 十二边形 D. 十四边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知∠α和∠β互为补角，且∠β比∠α小20°，则∠β等于_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是半圆的直径，点O是圆心，点C是OA的中点，CD⊥OA交半圆于点D，点E是
的中点，连接AE、OD，过点D作DP∥AE交BA的延长线于点P．（1）求∠AOD的度数；
（2）求证：PD是半圆O的切线．
-
科目： 来源： 题型：
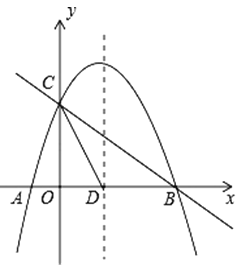
查看答案和解析>>【题目】如图，已知抛物线
与x轴交于A、轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求抛物线的表达式；
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数据2，3，5，7，3的极差是( )
A.2B.3C.4D.5
相关试题
