【题目】如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是![]() 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.

参考答案:
【答案】(1) 60°;(2)证明见解析.
【解析】试题分析:(1)根据CO与DO的数量关系,即可得出∠CDO的度数,进而求出∠AOD的度数;
(2)利用点E是![]() 的中点,进而求出∠EAB=30°,即可得出∠AFO=90°,即可得出答案.
的中点,进而求出∠EAB=30°,即可得出∠AFO=90°,即可得出答案.
试题解析:(1)∵AB是半圆的直径,点O是圆心,点C是OA的中点,
∴2CO=DO,∠DCO=90°,
∴∠CDO=30°,
∴∠AOD=60°;
(2)如图,连接OE,

∵点E是![]() 的中点,
的中点,
∴![]() ,
,
∵由(1)得∠AOD=60°,
∴∠DOB=120°,
∴∠BOE=60°,
∴∠EAB=30°,
∴∠AFO=90°,
∵DP∥AE,
∴PD⊥OD,
∴直线PD为⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和与外角和之和是1800°,则此多边形是( )
A. 八边形 B. 十边形 C. 十二边形 D. 十四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠α和∠β互为补角,且∠β比∠α小20°,则∠β等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.
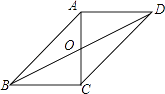
求:
(1)AC的长;
(2)求OB的长. -
科目: 来源: 题型:
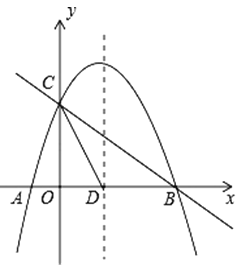
查看答案和解析>>【题目】如图,已知抛物线
 与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2,3,5,7,3的极差是( )
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形的三边长分别为3,4,x,则x的值可能是( )
A. 1 B. 6 C. 7 D. 10
相关试题

