【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.
(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
参考答案:
【答案】
(1)
证明:(1)连接OD.
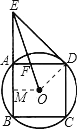
∵四边形ABCD为正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直线ED是⊙O的切线.
(2)
证明:作OM⊥AB于M,
∵O为正方形的中心,
∴M为AB中点,
∴AE=AB=2AM,AF∥OM,
∴ ![]()
∴EF=2FO.
【解析】(1)连接OD,只需证明OD⊥DE.根据正方形的性质得到AE=AD,则∠ADE=45°.又∠ADO=45°则证明了结论;(2)作OM⊥AB于M.根据平行线分线段成比例定理进行证明.
【考点精析】认真审题,首先需要了解正多边形和圆(圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
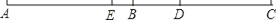
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则
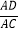 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+2的图象经过点(﹣1,4).
(1)求k的值;
(2)画出该函数的图象;
(3)当x≤2时,y的取值范围是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=x的图象为直线l.
(1)观察与探究
已知点A与A′,点B与B′分别关于直线l对称,其位置和坐标如图所示.请在图中标出C(4,﹣1)关于线l的对称点C′的位置,并写出C′的坐标_____;
(2)归纳与发现
观察以上三组对称点的坐标,你会发现:
平面直角坐标系中点P(a,b)关于直线l的对称点P′的坐标为_____;
(3)运用与拓展
已知两点M(﹣3,3)、N(﹣4,﹣1),试在直线l上作出点Q,使点Q到M、N两点的距离之和最小,并求出相应的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用“>”或“<”填空.
(1) 3.4 _____0 (2) 0 ______-22. 8
(3 ) -3______-4 (4) -
 ______-0.3
______-0.3 (5) -0. 66_____-
 (6) -
(6) -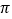 ______-3.14
______-3.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y=
 x+3的图象经过点B、C.
x+3的图象经过点B、C.
(1)点C的坐标为_____,点B的坐标为_____;
(2)如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=3,b=4,c=5; ②a=6,∠A=45°;③a=2,b=2,c=2
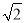 ; ④∠A=38°,∠B=52°.
; ④∠A=38°,∠B=52°.A. 1个 B. 2个 C. 3个 D. 4个
相关试题

