【题目】如图,点O为原点,A、B为数轴上两点,点A表示的数a,点B表示的数是b,且![]() .
.
![]()
(1)a= ,b= ;
(2)在数轴上是否存在一点P,使![]() ,若有,请求出点P表示的数,若没有,请说明理由?
,若有,请求出点P表示的数,若没有,请说明理由?
(3)点M从点A出发,沿![]() 的路径运动,在路径
的路径运动,在路径![]() 的速度是每秒2个单位,在路径
的速度是每秒2个单位,在路径![]() 上的速度是每秒4个单位,同时点N从点B出发以每秒3个单位长向终点A运动,当点M第一次回到点A时整个运动停止.几秒后MN=1?
上的速度是每秒4个单位,同时点N从点B出发以每秒3个单位长向终点A运动,当点M第一次回到点A时整个运动停止.几秒后MN=1?
参考答案:
【答案】(1)a=-8,b=4;(2)-1或6;(3)![]() 秒,
秒,![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)根据![]() ,利用绝对值及偶次方的非负性即可求出;
,利用绝对值及偶次方的非负性即可求出;
(2)若要满足![]() ,则点P在线段AB中点右侧,分三种情况讨论;
,则点P在线段AB中点右侧,分三种情况讨论;
(3)当MN=1时,根据运动情况,可分三种情形讨论,列出方程解答.
(1)解:(1)∵![]() ,
,
∴ab=-32,b-4=0,
∴a=-8,b=4.
(2)根据题意,若要满足![]() ,则点P在线段AB中点右侧,线段AB的中点表示的数为-2,设点P表示的数为x,分三种情况讨论:
,则点P在线段AB中点右侧,线段AB的中点表示的数为-2,设点P表示的数为x,分三种情况讨论:
①当-2≤x<0时,则x+8-(4-x)=2(-x),
解得:x=-1;
②当0≤x<4时,则x+8-(4-x)=2x,
方程无解
③当x≥4时,则x+8-(x-4)=2x,
解得:x=6.
综上:存在点P,表示的数为-1或6.
(3)设运动时间为t,根据运动情况,可知MN=1的情况有三种:
①M在A→O上,且M在N左侧,
则2t+3t+1=12,
解得t=![]() .
.
②M在A→O上,且M在N右侧,
则2t+3t-1=12,
解得t=![]() .
.
③M在O→A上,且N到达点A,
此时,M在A→O上所用时间为8÷2=4(s),
M在O→A上速度为4个单位每秒,
∵MN=1,
∴(8-1)÷4=![]() ,
,
∴此时时间t=4+![]() =
=![]() ,
,
综上:当MN=1时,时间为![]() 秒,
秒,![]() 秒或
秒或![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由7个同样大小棱长为1的小正方体搭成的几何体,请分别画出它的主视图、左视图和俯视图.
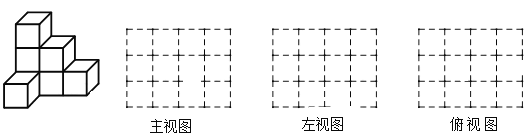
(2)这个组合几何体的表面积为 个平方单位(包括底面积);
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则搭这样的几何体最多要________个小立方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,∠AOC=48°,∠DOE∶∠BOE=5∶3,OF平分∠AOE.
(1)求∠BOE的度数;
(2)求∠DOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )

A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的“算筹”.算筹是古代用来进行计算的工具,它是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式(如图).

当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间:个位、百位、万位数用纵式表示;十位,千位,十万位数用横式表示;“0”用空位来代替,以此类推.例如3306用算筹表示就是
 ,则2022用算筹可表示为( )
,则2022用算筹可表示为( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
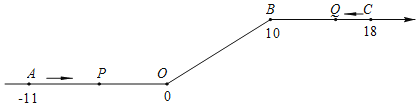
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
相关试题

