【题目】如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
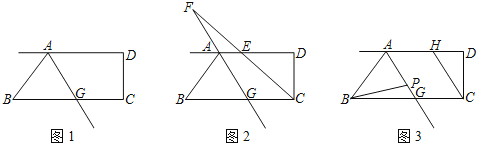
(1)求证:∠BAG=∠BGA;
(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点E、交射线GA于点F.求∠AFC的度数;
(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,请直接写出![]() 的值.
的值.
参考答案:
【答案】(1)详见解析;(2)20°或160°;(3)![]() 的值是5或
的值是5或![]() .
.
【解析】
(1)根据平行线的性质可得∠GAD=∠BGA,然后根据角平分线的定义可得∠BAG=∠GAD,最后利用等量代换即可求出结论;
(2)根据点E在线段AD上和点E在射线DA的延长线上分类讨论,根据画出对应的图形,然后根据角平分线的定义、平行线的性质和等量代换分别求出结论即可;
(3)根据点M在BP下方和BP上方分类讨论,分别画出对应的图形,设∠ABC=4x,
根据平行线的性质、三角形的内角和定理和角平分线的定义分别表示出∠ABM和∠GBM,即可求出结论.
(1)证明:∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD,
∴∠BAG=∠BGA;
(2)解:①若点E在线段AD上,
∵CF平分∠BCD,∠BCD=90°,
∴∠GCF=45°,
∵AD∥BC,
∴∠AEF=∠GCF=45°,
∵∠ABC=50°,
∴∠DAB=180°﹣50°=130°,
∵AG平分∠BAD,
∴∠BAG=∠GAD=65°,
∴∠AFC=65°﹣45°=20°;
②若点E在DA的延长线上,如图4,
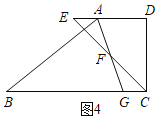
∵∠AGB=65°,∠BCF=45°,
∴∠AFC=∠CGF+∠BCF=115°+45°=160°;
(3)解:有两种情况:
①当M在BP的下方时,如图5,
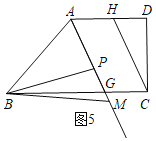
设∠ABC=4x,
∵∠ABP=3∠PBG,
∴∠ABP=3x,∠PBG=x,
∵AG∥CH,
∴∠BCH=∠AGB=![]() =90°﹣2x,
=90°﹣2x,
∵∠BCD=90°,
∴∠DCH=∠PBM=90°﹣(90°﹣2x)=2x,
∴∠ABM=∠ABP+∠PBM=3x+2x=5x,∠GBM=∠PBM-PBG=x
∴∠ABM:∠GBM=5x:x=5;
②当M在BP的上方时,如图6,
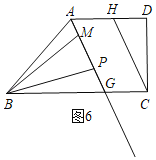
同理得:∠ABM=∠ABP﹣∠PBM=3x﹣2x=x,∠GBM=∠PBG+∠PBM=3x
∴∠ABM:∠GBM=x:3x=![]() .
.
综上,![]() 的值是5或
的值是5或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车
 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
-
科目: 来源: 题型:
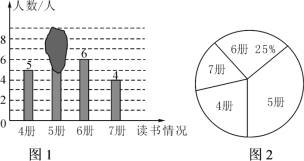
查看答案和解析>>【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,点A(0,0)、B(4
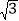 ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )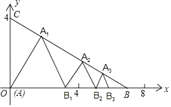
A.
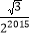 B.
B. 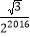 C.
C. 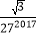 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直径为10的半圆O,tan∠DBC=
 ,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.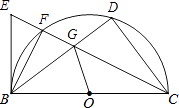
(1)求证:BE为⊙O切线;
(2)求证:BG2=FGCE;
(3)求OG的值. -
科目: 来源: 题型:
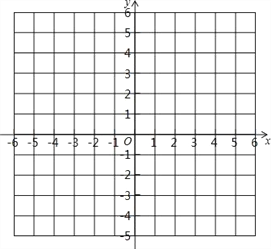
查看答案和解析>>【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣x+4与x轴交于点A,B,B点的坐标为(﹣4,0),与y轴交于点C.
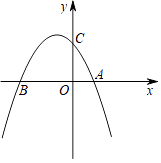
(1)求抛物线的解析式和对称轴.
(2)连接AC、BC,在x轴下方的抛物线上求一点M,使△ABM与△ABC的面积相等.
(3)在x轴下方作平行于x轴的直线l,与抛物线交于点D、E两点(点D在对称轴的左侧).过点D、E分别作x轴的垂线,垂足分别为G、F,当矩形DEFG中DE=2DG时,求D点的坐标.
相关试题

