【题目】在直角坐标系xOy中,ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.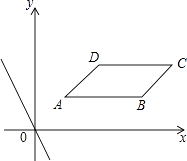
(1)k=;
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)-2
(2)解:设直线l的解析式是y=﹣2x+b,
把(2,2)代入得:﹣4+b=2,解得:b=6,
则直线l的解析式是y=﹣2x+6
(3)解:设过A直线l的解析式是y=﹣2x+b,把(1,1)代入得:﹣2+c=1,解得:c=3,
则直线的解析式是y=﹣2x+3,
同理,过C直线l的解析式是y=﹣2x+12,
则3≤b≤12
(4)解: 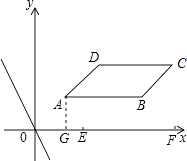
当直线l经过A时,解析式是y=﹣2x+3,令y=0,解得x= ![]() ,即与x轴的交点是E(
,即与x轴的交点是E( ![]() ,0);
,0);
当直线l经过C时,解析式是y=﹣2x+12,令y=0,解得x=6,即与x轴的交点是F(6,0);
当PA=PB时,P在AB的中垂线上,则P的坐标是( ![]() ,0);
,0);
当AP=AB=3时,则PG= ![]() =2
=2 ![]() ,则P的坐标是(2
,则P的坐标是(2 ![]() +1,0);
+1,0);
同理,当BP=BA=3时,P的坐标是(4﹣2 ![]() ,0).
,0).
故P的坐标是:( ![]() ,0)或(2
,0)或(2 ![]() +1,0)或(4﹣2
+1,0)或(4﹣2 ![]() ,0).
,0).
【解析】(1)根据已知直线l:y=kx+b与直线y=﹣2x平行.一次项系数相同,据此即可求得。
(2)设直线l的解析式是y=-2x+b,把D的坐标代入解析式即可求得b的值,即可得到函数的解析式。
(3)分别求得经过A和C的解析式,即可求得b的取值范围。
(4)先分别求出当直线l经过A时和当直线l经过C时的函数解析式,再当成PA=PB和AP=AB和BP=BA三种情况进行讨论即可求解。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
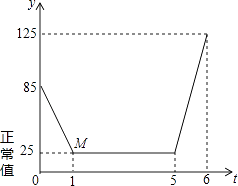
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2016+(3.14﹣π)0= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
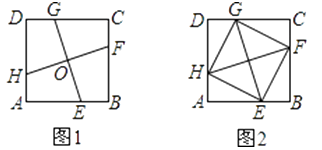
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三(6)班十几名同学毕业前和数学老师合影留念,一张彩色底片要0.6元,扩印一张相片0.5元,每人分一张,免费赠送老师一张(由学生出钱),每个学生交0.6元刚好,则相片上共有______人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
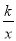 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>
 的解集.
的解集.有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>
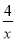 ;
;当x<0时,原不等式可以转化为x2+4x﹣1<
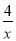 ;
;(2)构造函数,画出图象
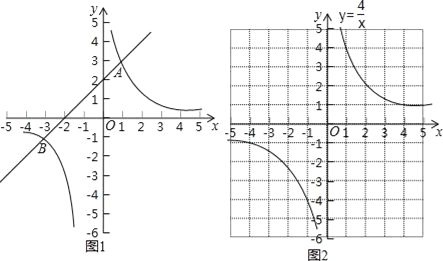
设y3=x2+4x﹣1,y4=
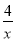 ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.双曲线y4=
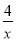 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(1)(5a-3b)-3(a-2b);(2)3x2-[7x-(4x-3)-2x2].
相关试题

