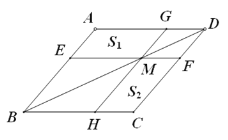
【题目】如图所示,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中平行四边形AEMG的面积![]() 与平行四边形HCFM的面积
与平行四边形HCFM的面积![]() 的大小关系是( )
的大小关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
根据平行四边形的性质和判定得出平行四边形GBEP、GPFD,证△ABD≌△CDB,得出△ABD和△CDB的面积相等;同理得出△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,相减即可求出答案.
∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中;
∵ ,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

-
科目: 来源: 题型:
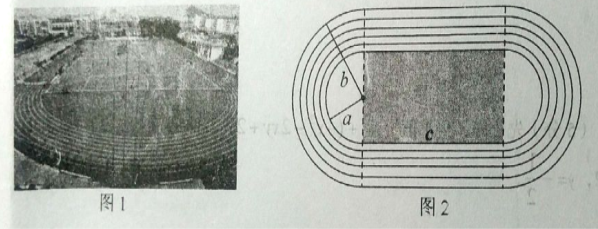
查看答案和解析>>【题目】综合与实践,
如图1是某校操场实物图,图2是操场示意图,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每两条跑道之间的距离是相等的,最内侧半圆形跑道的半径是a米,最外侧半圆形跑道的半径是b米,每条直道的长度都是c米。
(1)列式表示最内侧-圈跑道的长度____.(直接写出答案, 不写过程)
(2)列式表示整个操场所占地面的面积___ . (即最外侧跑道圈住的面积,直接写出答案,不写过程)
(3)新学期,学校为了给学生们提供优美的校园环境和锻炼场所,改造并美化操场,跑道内部的长方形部分(图中阴影部分)设计成足球场,这部分地面铺设草坪,其余部分(即矩形外部与最外侧跑道之间的部分)铺设塑胶.兴趣小组测得a=35米,b=40米,c=100米, π取3.若草坪每平米60元,塑胶每平米80元,请你计算铺设草坪和塑胶总共花了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律。则第(6)个图形中面积为1的正方形的个数为()

A. 20B. 25C. 35D. 27
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有 .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得 = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: + =( +
,填空: + =( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a是不为1的有理数,我们把
 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是 =﹣1,﹣1的差倒数是
=﹣1,﹣1的差倒数是 .已知a1=﹣
.已知a1=﹣ ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推.(1)分别求出a2,a3,a4的值;
(2)求a1+a2+a3+…+a3600的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
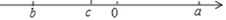
(1)用“>”“<”或“=”填空:
b______0,a+b______0,a-c______0,b-c______0;
(2)化简:|c-a|-|c-b|+|a+b|.
相关试题

