【题目】探索与研究:
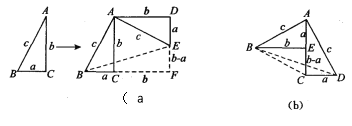
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
参考答案:
【答案】答案见解析
【解析】
试题分析:根据面积相等的法则进行计算.
试题解析:方法1:∵由图(a)可知S正方形ACFD=S四边形ABFE ,
∴S正方形ACFD=S⊿BAE+S⊿BFE
又∵正方形ACFD的边长为b, SRt△BAE=![]() ,SRt△BFE=
,SRt△BFE=![]()
∴b2 =![]() +
+![]()
即2b2 =c2 +(b+a)(b-a)
整理得: a2 +b2=c2
方法2:如图(b)中,Rt△BEA和Rt△ACD全等, 设CD=a,AC=b,AD=c(b>a),
则AE=a,BE=b,AB=c,EC=b-a
由图(b),S四边形ABCD = SRt△BAE + SRt△ACD+SRt△BEC =SRt△BAD+S△BCD
又∵ SRt△BAE =![]() , SRt△ACD =
, SRt△ACD = ![]() ,SRt△BEC =
,SRt△BEC =![]() ,
,
SRt△BAD=![]() ,S△BCD=
,S△BCD=![]() ,
,
∴![]() +
+![]() +
+![]() =
=![]() +
+ ![]()
即2ab+b(b-a) = c2 +a(b-a)
整理得: a2 +b2=c2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a2·a3=a5 B. (a2)3=a5 C. a6÷a2=a3 D. a6-a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数
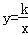 的图象上.那么k的值是 .
的图象上.那么k的值是 .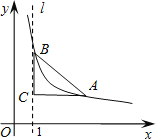
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
-
科目: 来源: 题型:
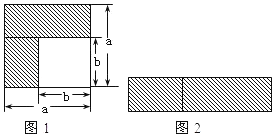
查看答案和解析>>【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
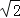 ≈1.41,
≈1.41,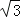 ≈1.73,结果保留整数)
≈1.73,结果保留整数)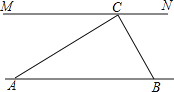
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是

A. (-4,2) B. (-4.5,2) C. (-5,2) D. (-5.5,2 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
相关试题

