【题目】乘法公式的探究及应用.
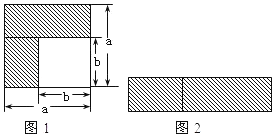
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
参考答案:
【答案】(1)a2﹣b2(2)a﹣b,a+b,(a+b)(a﹣b)(3)99.96(4)①99.96②4m2﹣n2+2np﹣p2
【解析】
试题分析:(1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.2)×(10﹣0.2),
=102﹣0.22,
=100﹣0.04,
=99.96;
②解:原式=[2m+(n﹣p)]×[2m﹣(n﹣p)],
=(2m)2﹣(n﹣p)2,
=4m2﹣n2+2np﹣p2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与研究:
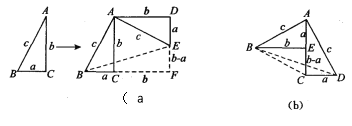
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
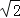 ≈1.41,
≈1.41,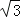 ≈1.73,结果保留整数)
≈1.73,结果保留整数)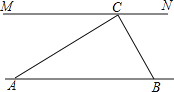
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是

A. (-4,2) B. (-4.5,2) C. (-5,2) D. (-5.5,2 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个零件的形状如图所示,按规定∠A=90,∠C=25,∠B=25,检验员已量得∠BDC=150,请问:这个零件合格吗?说明理由。
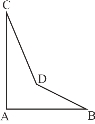
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)邮递员一共骑了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的余角是30,则这个角的大小是______.
相关试题

