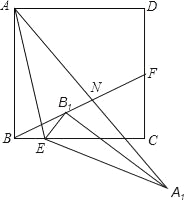
【题目】如图,正方形ABCD中,AB=4,点E是BC上一点,且tan∠BAE=![]() ,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
(1)求证:∠BFC=∠A1 B1F;
(2)说明点N是AA1的中点;
(3)求AN的长.
参考答案:
【答案】(1)详见解析; (2)详见解析;(3)![]() .
.
【解析】试题分析:(1)已知四边形ABCD是正方形,根据正方形的性质可得AB∥CD,即可得∠ABF=∠CFB,由旋转的性质可得EB=EB1,根据等腰三角形的性质可得∠EBB1=∠EB1B,再由∠ABC=∠EB1A1=90°,即可得∠ABF+∠EBB′=90°,∠BB1E+∠A1B1F=90°,所以∠A1B1F=∠ABF=∠BFC;(2)作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,可得点P是BB1的中点,根据三角形的中位线定理可得EP∥MB1,即可得MB1⊥BB1;易证△BPE∽△BCF,即可求得BP=![]() ,EP=
,EP=![]() ,从而求得BB1=
,从而求得BB1=![]() ,再证明A,B1,M三点共线,即可得AB1=
,再证明A,B1,M三点共线,即可得AB1=![]() ,再证明△AB1N≌△A1QN,即可得AN=A1N,从而证得N是AA1的中点;(3)由△AB1N≌△A1QN,可得B1N=
,再证明△AB1N≌△A1QN,即可得AN=A1N,从而证得N是AA1的中点;(3)由△AB1N≌△A1QN,可得B1N=![]() B1Q=
B1Q=![]() ,根据勾股定理即可求得AN=
,根据勾股定理即可求得AN=![]() .
.
试题解析:
(1)∵四边形ABCD是正方形,
∴AB∥CD,
∴∠ABF=∠CFB,
∵EB=EB1,
∴∠EBB1=∠EB1B,
∵∠ABC=∠EB1A1=90°,
∴∠ABF+∠EBB′=90°,∠BB1E+∠A1B1F=90°,
∴∠A1B1F=∠ABF=∠BFC.
(2)作EP⊥BF,A1Q⊥BF,取BC的中点M,连接AB1,B1M,
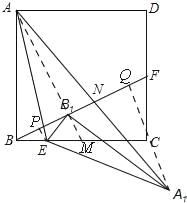
∴点P是BB1的中点,
∵E是BM中点,
∴EP∥MB1,
∴MB1⊥BB1,
由旋转得,△BPE∽△BCF,
∴BP=![]() ,EP=
,EP=![]() ,
,
∵PB1=PB=![]() ,
,
∴BB1=![]() ,
,
∵sin∠FBC=![]() =
=![]() =
=![]() ,
,
∴∠AB1B=90°,
∴A,B1,M三点共线,
∴AB1=![]() ,
,
∵∠B1A1Q=∠BB1E=∠FBC,
∴△B1QA1∽△FCB,
∴B1Q=![]() ,A1Q=
,A1Q=![]() =AB1,
=AB1,
∴△AB1N≌△A1QN,
∴AN=A1N,
∴N是AA1的中点.
(3)∵△AB1N≌△A1QN,
∴B1N=![]() B1Q=
B1Q=![]() ,
,
根据勾股定理得,AN=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线y=x+b与双曲线y=
 (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

-
科目: 来源: 题型:
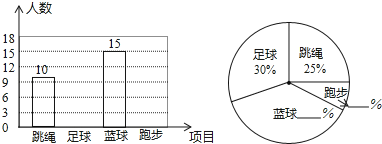
查看答案和解析>>【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如图不完整的条形统计图和扇形统计图(部分信息未给出)
(1)求本次调查学生的人数.
(2)求喜爱足球、跑步的人数,并补全条形统计图;
(3)求喜爱篮球、跑步的人数占调查人数的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).
(1)观察一个等比列数1,
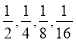 ,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以
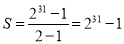
请根据以上的解答过程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示an;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+an.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠2.
(1)判断四边形AECF的形状,并证明你的结论.
(2)若AE=4,AF=2,试求菱形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,矩形OABC放置于平面直角坐标系中,点O与原点重合,点A在x轴正半轴上,点C在y轴正半轴上,点B的坐标为(6,3),点D是边BC上的一动点,连接OD,作点C关于直线OD的对称点C′.
(1)若点C、C′、A在一直线上时,求点D的坐标;
(2)若点C′到矩形两对边所在直线距离之比为1:2时,求点C′的坐标;
(3)若连接BC′,则线段BC′的长度范围是 .

-
科目: 来源: 题型:
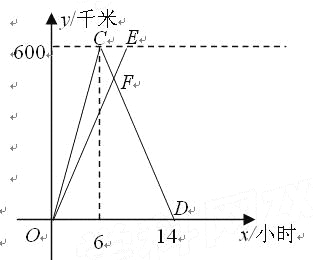
查看答案和解析>>【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
相关试题

