【题目】已知如图,矩形OABC放置于平面直角坐标系中,点O与原点重合,点A在x轴正半轴上,点C在y轴正半轴上,点B的坐标为(6,3),点D是边BC上的一动点,连接OD,作点C关于直线OD的对称点C′.
(1)若点C、C′、A在一直线上时,求点D的坐标;
(2)若点C′到矩形两对边所在直线距离之比为1:2时,求点C′的坐标;
(3)若连接BC′,则线段BC′的长度范围是 .

参考答案:
【答案】(1)D(![]() ,3);(2)点C′的坐标为(
,3);(2)点C′的坐标为(![]() ,2)或(2
,2)或(2![]() ,1);(3)3
,1);(3)3![]() ﹣3≤BC′≤6.
﹣3≤BC′≤6.
【解析】试题分析:(1)根据轴对称的性质和矩形的性质易证∠DCE=∠COD,再求得CD的长,即可得点D的坐标;(2)分点C′到矩形OA边与BC边的距离之比为1:2和点C′到矩形BC边与OA边的距离之比为2:1两种情况求点C′的坐标即可;(3)由OC′=OC,可知点C′在以O为圆心,以3为半径的弧上(如图).当点D与点C或点B重合时,BC′有最大值.当点C′在直线OB上时,BC′有最小值.由此即可求得BC的取值范围.
试题解析:
(1)如下图所示:

∵点C、C′、A在一直线上,
∴tan∠BCC′=![]() =
=![]() .
.
∵点C与点C′关于OD对称,
∴OD⊥CC′.
∴∠DCE+∠CDE=90°.
∵∠CDE+∠COD=90°.
∴∠DCE=∠COD.
∴tan∠COD=![]() =
=![]() ,
,
∴CD=![]() OC=
OC=![]() .
.
∴D(![]() ,3).
,3).
(2)设点C′的坐标为(x,y).
由轴对称的性质可知OC=OC′=3.
由两点间的距离公式可知x2+y2=9.
点C′到矩形两对边所在直线距离之比为1:2时,
C′的纵坐标为2或1.
将y=2代入x2+y2=9得:x2+4=9,解得:x=![]() 或x=﹣
或x=﹣![]() (舍去),
(舍去),
∴C′(![]() ,2).
,2).
将y=1代入x2+y2=9得:x2+1=9,解得:x=2![]() 或x=﹣2
或x=﹣2![]() (舍去),
(舍去),
∴C′(2![]() ,1).
,1).
综上所述,点C′的坐标为(![]() ,2)或(2
,2)或(2![]() ,1).
,1).
(3)∵OC′=OC,
∴点C′在以O为圆心,以3为半径的弧上.
如下图所示:

当点D与点C或点B重合时,BC′有最大值,最大值=BD=6.
当点C′在直线OB上时,BC′有最小值.
在△ABO中,依据勾股定理可知OB=![]() =3
=3![]() .
.
∵OC′=OC=3,
∴BC′的最小值=BO﹣OC′=3![]() ﹣3.
﹣3.
∴线段BC′的长度范围是3![]() ﹣3≤BC′≤6.
﹣3≤BC′≤6.
故答案为:3![]() ﹣3≤BC′≤6.
﹣3≤BC′≤6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).
(1)观察一个等比列数1,
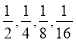 ,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以
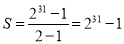
请根据以上的解答过程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示an;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+an.
-
科目: 来源: 题型:
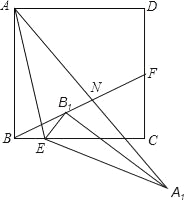
查看答案和解析>>【题目】如图,正方形ABCD中,AB=4,点E是BC上一点,且tan∠BAE=
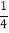 ,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.
,点F是CD的中点,连接AE、BF将△ABE着点E按顺时针方向旋转,使点B落在BF上的B1处位置处,点A经过旋转落在A1点位置处,连接AA1交BF于点N.(1)求证:∠BFC=∠A1 B1F;
(2)说明点N是AA1的中点;
(3)求AN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠2.
(1)判断四边形AECF的形状,并证明你的结论.
(2)若AE=4,AF=2,试求菱形ABCD的面积.

-
科目: 来源: 题型:
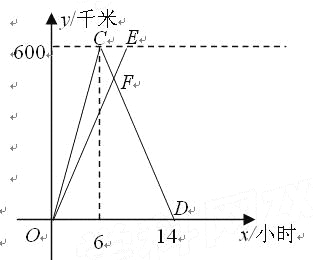
查看答案和解析>>【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B.
 ﹣1 C.
﹣1 C.  D. 2﹣
D. 2﹣
相关试题

