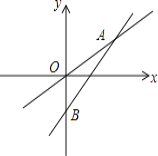
【题目】如图所示是一个正比例函数与一个一次函数的图象，它们交于点A (4，3)，一次函数的图象与y轴交于点B，且OA=OB.

（1）求这两个函数的解析式；

（2）当x取何值时，一次函数的值大于正比例函数的值？

参考答案：

【答案】（1）y=0.75x，y=2x-5 ；（2）x>4.

【解析】试题分析：

（1）由点A的坐标为（4，3）可求得正比例函数的解析式和线段OA的长度，从而可得OB的长度，由此可得点B的坐标，由点A、B的坐标即可求得一次函数的解析式；

（2）由图可知，在点A的右侧，一次函数的图象在正比例函数图象的上方结合点A的坐标为（4，3）即可得到本题答案.

试题解析：

（1）设正比例函数的解析式为： ；一次函数的解析式为： ；

∵点A的坐标为（4，3），且点A在正比例函数的图象上，

∴OA=， ，解得： ，

∴OB=OA=5，正比例函数的解析式为： ；

∴点B的坐标为： ，

把点A、B的坐标代入得： ，解得： ，

∴一次函数的解析式为： ；

（2）由图可知，在点A的右侧，一次函数的图象在正比例函数图象的上方，

∴当时，一次函数的值大于正比例函数的值.

关闭